где W И дш)/дх определяют изгиб в направлении х. Кроме того, заметим, что разложение для w представляет собой кубический полином. Из опыта с изгибом балки ясно, что заданные на концах четыре степени свободы (wi, w, Qy, 9J из общего числа степеней свободы полностью определяют вариацию w и dw/dx вдоль этой границы. Однако наклон нормали dw/dy описывается кубической функцией, и, так как для определения этой функции остались всего лишь две степени свободы 6 и 9, то она определяется неоднозначно. Поэтому решение, полученное с использованием элементов указанного типа, не будет доставлять минимум потенциальной энергии. С другой стороны, имеются теоретические обоснования сходимости решения для этого типа элементов (см., например, [12.13]). Матрица жесткости элемента, отвечающая этой функции, задана в табл. 12.1 (см. стр. 389-391).

Исследуя изображенный на рис. 12.4 треугольник Паскаля, можно выбрать различные альтернативные представления. Существуют также соответствующие альтернативы при построении полей перемещений с использованием функций формы. В работе [12.9] приводится ряд функций формы для представлений с двенадцатью степенями свободы. В [12.10] и [12.11] обсуждаются альтернативные степенные поля перемещений с 16 степенями свободы, в [12.8, 12.12] и др. формируются прямоугольные элементы для пластин с более чем 16 степенями свободы.

12.2.2. Предполагаемые модели перемещения - метод подобластей

Альтернативные построения, основанные на предполагаемых полях перемещений, можно осуществить, разбивая четырехугольный элемент на четыре треугольных элемента и задавая независимо поля перемещений в каждом из треугольников. Далее треугольные элементы объединяют, чтобы получить четырехугольный элемент посредством задания условий непрерывности перемещений вдоль внутренних границ, определяемых разбиением на подобласти.

В работе [12.14] предложен этот подход при формулировке межэлементно согласованного элемента с 16 степенями свободы. Внутри каждого треугольника выбирается полное кубическое (10 членов) полиномиальное представление поля перемещений. Традиционное задание трех степеней свободы (перемещение и два вращения) в углах дополняется заданием вдоль каждой стороны одной степени свободы в виде углового перемещения.

Аналогичный подход был предложен в работе [12.15], где на основе принципа минимума потенциальной энергии построен четырехугольный элемент путем соответствующего объединения четырех треугольных элементов. Здесь треугольные элементы сами строятся посредством разбиения элемента на три треугольные подобласти (формулировка этих треугольников описывается в п. 12.3.2).

Следует отметить, что, прежде чем составлять из треугольников четырехугольный элемент, стороны которого становятся внешними границами, задаются условия, обеспечивающие исключение степеней свободы в серединах указанных сторон. Таким образом, в окончательном варианте четырехугольный элемент имеет всего 12 степеней свободы (по три в каждом углу). Условия внутренней и межэлементной согласованности для этого элемента выполняются.

12.2.3. Обобщенный вармацмонный подход

Обобщенный вариационный подход, описанный в гл. 6 и 7, особенно привлекателен при формулировках изгиба пластин. Так как трудно определить и оперировать с полями поперечных перемещений, которые полностью межэлементно согласованы, желательно выбрать удобное поле, которое не удовлетворяет этим условиям, и далее навязать условие непрерывности, задавая ограничения. Для две-надцатичленной функции (12.27), например, необходимо обеспечить лишь непрерывность угловых перемещений. Довольно глубокие исследования в этой области четырехугольных изгибаемых элементов можно найти в статьях [12.16, 12.17]. Этот подход обсудим для треугольных элементов в разд. 12.13.

12.2.4. Смешанные формулировки в напряжениях и перемещениях

В работах [12.18, 12.19] исследованы гибридные формулировки в напряжениях для прямоугольных элементов, а формулировки для четырехугольных элементов даны в [12.20]. В каждой используется схема с единственным полем. В [12.21] приведены две альтернативные формулировки путем разбиения элемента на подобласти и с использованием гибридной схемы в напряжениях.

Подход на базе функционала Рейсснера, модифицированный, как описано в разд. 12.2, Херрманом [12.7], был применен в работе [12.22] для различных четырехугольных элементов как для представления единственным полем, так и при разбиении элемента на подобласти.

12.2.5. Предполагаемые поля напряжений

Как было указано, для функционала дополнительной энергии, выраженного в терминах функции напряжений Саусвелла, требуются те же поля, что и при описании перемещений, если анализировать плоско-напряженное состояние на основе подхода, использующего принцип минимума потенциальной энергии. Поэтому рассуждения, касающиеся последней темы из разд. 9.3, справедливы и в данно.м случае. Результаты подсчетов с использованием указанного подхода приведены в [12.23].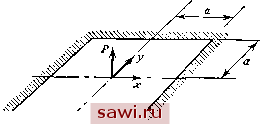

Рис. 12.5. Квадратная жестко защемленная п.пастина.

исследовать эту задачу, используя лишь один элемент для четверти пластины, введя при этом лишь одну степень свободы: перемещение Wi под сосредоточенной силой. В этом случае Pi=kiiWT, PPi/4, Х2=Уз=й. Согласно табл. 12.1 (см. стр. 389), для формулировки с использованием 12 членов имеем

Т = 360(У??1[120(1 + 1)-24 + 84]ш

или, полагая D=£/V12(l-р,=), а=0.3, имеем WfO.0237 (аРЮ). Используя коэффициенты жесткости из [12.8] для шестнадцатичлен-ной формулировки, получим Wi=0.02l2{aPi/D).

Точное решение [12.2] равно 1=0.0224 (aPi/D), поэтому каждое из решений приблизительно на 8% отличается от точного, находясь по разные стороны от него. Как и предполагалось, согласованное (шестнадцатичленное) решение ограничивает снизу точное решение.

На рис. 12.6 представлена задача, рассматриваемая при сравнении различных формулировок пластинчатых элементов при изгибе. В задаче определяются перемещения, вызванные действием сосредоточенной силы, приложенной в центре свободно опертой пластины. Приводимые графики вычислений отражают зависимость возникающей при численном определении перемещений ошибки от размеров сетки разбиения квадранта пластины.

Следует отметить, что представленные результаты не обязательно определяют нужные параметры для сравнения точности н эффективности, так же как и размеры ячейки не обязательно являются наиболее точной мерой затраченных усилий Такие величины, как напряжение или энергия деформации, являются более существен-

12.2.6. Сравнение численных результатов

Рассмотрим вначале жестко закрепленную квадратную пластину 2аХ2а, на которую в центре действует сосредоточенная сила Pt (рис. 12.5). Учитывая симметрию относительно двух осей, можно