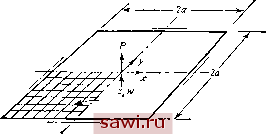
Рис. 12.6. Задачи для сравнения вычислительных аспектов, (а) Сетки для прямоугольных элементов; (Ь) сетки для треугольных элементов. Показаны лишь представительные образцы сеток. Здесь также используются сетки, повернутые на 90°.

НЫМИ параметрами, характеризующими поведение конструкции. Наиболее предпочтительной мерой затраченных усилий могли бы служить такие факторы, как затрачиваемые усилия при программировании алгоритма, затраты на решение системы уравнений и интерпретацию полученных результатов. Например, те же самые величины, но в зависимости от других характеристик эффективности были приведены в работе [12.241. В данной главе графики главным образом приводятся для того, чтобы выяснить верхнюю и нижнюю границы решений, продемонстрировать сходимость и оцепить альтернативы внутри ограниченного числа форм элементов и процедур их построения.

На рис. 12.7 приведены результаты для различных формулировок прямоугольных элементов. Заметим, что двенадцатичленный полином стремится к точному решению сверху, так как условия межэлементной непрерывности перемещений нарушаются, характеристика, соответствующая нижней границе , которая получается с использованием принципа минимума потенциальной энергии, не достигается. Наоборот, формулировка с использованием шестнад-цатичленного полинома и разбиения элемента па подобласти, предложенная в работе [12.14 , обусловливает сходимость и обеспечивает достижение нижней границы для получающихся решений. На этом же рисунке приведены результаты для двух формулировок

I с

1 2 3 4 6 ~

Разпернасть сетка {см. рис, 12.6)

Рис. 12.7. Сравнение численных результатов: четырехугольные конечно-элементные формулировки; / - смешанная формулировка с линейными М к w [12.22]; 2 - двенадцатичленный полином (12.32); 3 - смешанная формулировка с квадратичными М пш [12.22]; 4 - шестнадцатичленный полином [12.31]; 5 - согласованные четырехугольные подобласти [12.14].

на базе модифицированного функционала Рейсснера [12.22]. В одной из них вводится линейное поле изгибающих моментов и поле граничных поперечных смещений. В другой используются квадратичные функции. Очевидно, что существенное увеличение точности вытекает из увеличения порядка этих функций.

12.3. Треугольные элементы

12.3.1. Формулировки в перемещениях- единственное поле

На рис. 12.8 представлены различные способы задания степеней свободы для треугольного пластинчатого элемента прн изгибе, обусловленные различным выбором членов в полиномиальном представлении поперечного смещения w.

Желательный вид треугольного пластинчатого элемента при изгибе показан на рис. 12.8(a). Этому элементу отвечают сила в направлении г и по два изгибающих момента в каждой вершине. Узлы внутри элемента и на его границах между вершинами отсутствуют. Он характеризуется девятью степенями свободы и поэтому требует девятичленного разложения для w. Однако из рассмотре-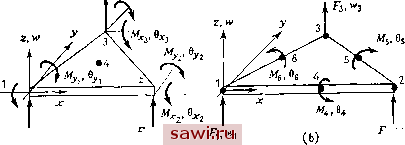

ui (а)

Тит/чная i/3/7oSair степень сЗоаоЗы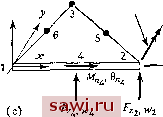

Рис. 12.8. Конечно-элементное представление треугольными элементами с единственным полем, (а) Треугольник с девятью степенями свободы (если задано 4, то число степеней свободы равно 10: w=af-\-a2X-\-. . .-\-Щ(1у);(Ъ) треугольник с шестью степенями свободы {wa-l-ax-i-. . .-{-ау); (с) треугольник с двадцатью одной степенью свободы (cci=a,-f-a2Jc-f-. . .-{-агУ).

ния треугольника Паскаля следует, что полный полином содержит либо 6 членов (квадратичный), либо 10 членов (кубический). Чтобы получить девятичленное разложение, можно объединить пару членов [например, ag(x+y)xy], однако можно убедиться, что для некоторых форм элемента преобразование от обобщенных степеней свободы к узловым становится вырожденным. Поэтому выбор 9 членов не может быть осуществлен с помощью полиномиальных разложений, которые для заданного порядка полны.

Если невзирая на полноту выбирается полином с 9 членами, то нарушаются условия геометрической изотропии . Например, мож-