12.3.2. Сравнение численных результатов. Формулировки в перемещениях - единственное поле

Сравнение численных результатов для формулировок с единственным полем, о которых шла речь, проводится на рис. 12.9 для свободно опертой квадратной пластины, нагруженной в центре сосредоточенной силой.

Ра2пер сеты

Рис. 12.9. Сравнение численных результатов: треугольные элементы с единственным полем. / ~ шестичленный (квадратичный) полином [12.27]; 2 - несогласованные поля [12.25]; 3 - двадцатиодночленный полином (пятой степени) [12.34]; 4 - десятнчленный (кубический) полином с ограничениями [12.28 ]; 5 - десяти-членпый (кубический) полином с корректирующей матрицей [12.17]; 6 - Разак (А-9) [12.26]; 7 - согласованные поля [12.25]. Размер сетки взят из рис. 12.6.

Заметим сначала, что элемент с шестью степенями свободы (полный квадратичный полином) [12.27] обусловливает сходн.мость к решению сверху, т. е. это решение является верхней границей.

Это происходит потому, что решение полностью согласуется с условиями равновесия. Результат довольно неточен для заданных значений параметров сетки, хотя, с другой стороны, матрица жесткости элемента имеет довольно простой вид. Действительно, можно в явном виде выписать эту матрицу жесткости без значительных усилий.

Численные результаты для элемента, основанного на полном кубическом полиноме, относятся лишь к случаю задания ограничений, обеспечивающих сохранение непрерывности угловых перемещений при переходе через границу элемента Результаты, полученные без задания ограничений, настолько неточны, что соответствующие им графики не помесгились в представленном на рисунке диапазоне изменения величин. Как можно ожидать, решения, полученные либо путем наложения соответствующих ограничений на каждой границе между соседними элементами [12.28], либо путем введения корректирующей матрицы жесткости с использованием обобщенного вариационного принципа [12.17], очень близки.

Однако здесь все же приведены результаты, полученные с помощью элементов, основанных на кубических функциях формы, выраженных в терминах треугольных координат (12.35), откуда исключен член, содержащий LxLiLa (т. е. формулировка, построенная Бейзли и др.) [12.25]. Принимая во внимание простоту этого элемента, можно заключить, что полученные численные результаты превосходные. Тем не менее следует отметить, что точность получаемых результатов зависит от геометрии конечно-элементной сетки [12.25].

Результаты для формулировок, основанных на полных полиномах 5-й степени (21 член), очень точны. Результаты для случая, когда узлы в серединах сторон исключены перед проведением расчетов, не приведены, потому что они отличаются незначительно. Затраты на формулировку этих элементов вполне существенны, и вновь следует упомянуть, что торговля между затратами на построение элемента и размерами сетки, не представленная на рис. 12.9, должна учитываться при любых практических обстоятельствах.

12.3.3. Формулировки с использованием предполагаемых перемещений. Метод разбиения на подобласти

Работа [12.38] послужила толчком к построению матриц жесткости треугольных элементов для расчета изгиба пластин на базе метода разбиения на подобласти, в котором элемент разбивается на треугольные подэлементы. Эти авторы использовали неполный (девя-тичленный) кубический полином в каждом из трех подэлементов, выбирая систему координат в каждом подэлементе так, чтобы не возникли трудности из-за отсутствия геометрической изотропии, и в том виде, чтобы обеспечить квадратичный характер изменения

перемещений вдоль каждой стороны, которая станет внешней для всего элемента.

Улучшенный вариант этой формулировки подразумевает использование полного кубического полинома (10 членов) внутри каждой подобласти. Поэтому основных степеней свободы всего 30 и число их уменьшают до 12 - девять степеней свободы в вершинах и угловые смещения в середине каждой стороны - налагая условия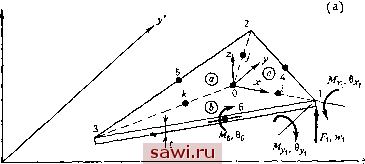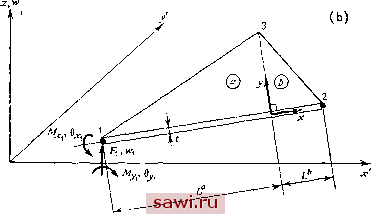

Рис. 12.10. Треугольные элементы - разбиение на подобласти: (а) треугольник с тремя подобластями; (Ь) треугольник с двумя подобластями.

непрерывности перемещений при переходе через границы подэле-ментов. Ниже эта формулировка описывается подробно.