сравнению с формулировкой с 9 степенями свободы, приходящимися на подэлемент. Интересно отметить, что последняя формулировка приводит к матрице жесткости (и конечно, к численным результатам), совпадающей с полученной Бейзли и др. [12.25] для треугольного согласованного элемента с единственным полем (ср. с решением, приведенным на рис. 12.9). Применение СРТ-элементов обусловливает вполне приемлемую точность для рассматриваемого круга задач.

12.3.5. Формулировки в напряжениях

Если выражение для дополнительной энергии записывается в терминах функций напряжения Саусвелла Ф и Ф, как это сделано в разд. 12.1.3, то выбор представлений для этих функций напряжения аналогичен выбору полей перемещений и и у в случае плосконапряженного состояния. Поэтому для треугольного элемента, у которого степени свободы заданы в вершинах, функции напряжений можно аппроксимировать в виде [12.40]

фя=Л,Ф5+ЛаФ+ЛзФ, Ф=Л1Ф?+Л2Ф2 +ЛзФ?, (12.44)

где Ni=Lu N2=L2, Мз=Ьз и Lj, Lj, Lg - треугольные координаты, введенные в гл. 8. Если же треугольный элемент задан с помощью степеней свободы в вершинах (обозначенных как точки 1, 2, 3)

г 4 6 8

Размер сетки (см. рис. 12.6)

Рис. 12.12. Сравнение численных результатов: для треугольных элементов, основанных на уравновешенных полях напряжений, и треугольных элементов, осно-ъанных на совместимых полях перемещений. / - формулировка, базирующаяся на уравновешенных полях напряжений [12.40] (линейные поля функций напряжения); ? - формулировка, основанная на совместимых полях перемещений [12.38] (девятичленный полином в подобласти).

н В серединах сторон (точки 4, 5, 6), то соответствующее разложение для Ф и Ф имеет вид [12.41]

фи=[ NJ{Ф}, Ф=LNJ{Ф),

(12.45)

где N J = [ AljVa. . .jV J с элементами, определенными в разд. 8.5,

{Ф }=[ Ф Ф; ... ФXJ {Ф)=[ ФФ ... Ф?jt.

Теперь, чтобы построить матрицу податливости элемента, необходимо выполнить операции, соответствующие (12.19) - (12.23).

Очевидные преимущества применения подхода к анализу изгиба пластин снижаются в значительной степени трудностью задания нагрузок. Следует напомнить, что интеграл по границе в выражении для дополнительной энергии зависит от задаваемых перемещений, которые обычно полагаются равными нулю. Граничные условия на нагруженной поверхности должны учитываться особым образом, обычно посредством наложения уравнений связи. Подсчет перемещений также представляет определенные трудности. Эти и некоторые другие аспекты практического использования данного подхода описаны в [12.23] и 12.40-12.42].

На рис. 12.12 даны результаты расчета свободно опертой квадратной пластины, в центре которой приложена сосредоточенная сила; расчет основан на линейных полях (12.44). Для сравнения приведены численные результаты для межэлементно согласованных формулировок для перемещений, полученных на базе метода разбиения на подобласти с использованием девятичленного полипома в каждой подобласти [12.381. Результаты, как и следовало ожидать, подтверждают, что решения, полученные с помощью альтернативной формулировки, основанной на принципе минимума дополнительной энергии, сходятся к точному решению снизу и обеспечивают достаточную точность.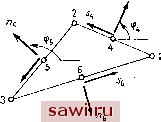

Рис. 12.13. Треугольный изгибаемый элемент для смешанной (llj) формулировки-линейное поле перемеш,ений и постоянное поле моментов.

12.3.6. Смешанные поля перемещений и напряжений

Модифицированная форма вариационного принципа Рейсснера, заданная формулами (12.24)-(12.27), представляет характерную формулировку, основанную на смешанных полях перемещений и напряжений для изгибаемых пластинчатых элементов, и подробно описывается ниже для случая простейшего треугольного элемента (рис. 12.13). Предположим, что прогибы описываются линейным полем, а компоненты внутренних изгибающих моментов являются константами. Тогда

где Л1, Л2, Лз - функции формы, введенные в (12.44). Кроме того, Шх=а1, Шу=а2, Шху=аз, где аг и аз - константы. Чтобы выразить эти константы через физические параметры, определим нормальные изгибающие моменты Mi, М, и в серединах сторон. Оценив изгибающие моменты Мх, М, Мху и разрешив относительно йи Ui, из, получим соотношение (12.26) (т. е. a)t=[NmJ{M}), б котором

созФ sin% 2 sin cos ф

[Nj]= СОЗфб ЗШф, 2 81ПфбС03фб

cos ф slnфв 2 sin ф, cos фа

Углы Ф4, Фб, фв определяются согласно рис. 12.13. Необходимо также получить выражение для тангенциальных моментов = [.sys,s,J как функций от {М}. Для этого можно сначала записать Яв как функцию от 9И в виде a)f,=[rj9 , где

~-81ПфС03ф4 31Пф4С05ф соз2ф

[Г] = - sin Ф5 cos ф, sin Ф5 cos Ф5 cos 2ф5 - sin Фв cos Фв sin Фв cos ф, cos 2фв

откуда следует, что a ,=[rj[Nj]{M}=[L]{M}.

Как показывает соотношение (12.24Ь), дискретизованное выражение рассматриваемого функционала Пн содержит матрицы [Qi2l=[fl2iF и [йц], которые в свою очередь построены с использованием матриц [Nд,], [Nm], [Na,], Ши,\, iLl и [Y], где штрихом обозначена операция дифференцирования базисных матриц [N] и [N ] в соответствии с определением, данным в п. 12.1.4. Кроме того, матрица [Y] получается в результате аналогично определенных операций дифференцирования поля перемещений. Так как [N ,1 - матрица, элементы которой являются константами, то [N,;j = l0]