при 2, отсчитываемом от срединной линии. Имеем следующее выражение:

Edx. (13.5)

Далее, чтобы преобразовать выписанные выражения в соотношения линейной теории устойчивости, опустим член более высокого порядка {AI){dwldxY и заметим, что при предположенин о возможности независимого анализа напряженного состояния до наступления выпучивания осевая сила связана с осевой деформацией линейным соотношением

Рх = ЕА, (13.6)

где величина f положительна при растяжении. Поэтому выражение (13.5) приводится к виду

Таким образом, выражение для энергии деформации приводится к форме, в которой энергии осевой и изгибной деформации не связаны друг с другом, т. е.

и=иа+Щ, (13.8)

(13.10)

Здесь энергия Ua относится к осевым деформациям, реализованным перед наступлением выпучивания.

Можно теперь сосредоточить внимание на случае изгибной деформации, предполагая, что решение для осевой силы находится независимо, согласно принципу минимума потенциальной энергии.

Используя концепции гл. 6, можно выписать уравнение Эйлера для функционала (13.10) в виде

- - ОЗ.П)

* dx

= 0.

Это хорошо известное уравнение, описывающее выпучивание балки.

Принимается следующее функциональное представление для поперечных смещений в терминах четырех узловых смещений:

9. 10.

= LNJ{A,}.

(13.12)

На этом этапе не используется какой-либо особый вид функции формы L J > при этом подразумевается, что функция формы, которая точно применима для изгиба балки, не удовлетворяет строго дифференциальному уравнению, отвечающему данному случаю (уравнение (13.11)).

Подставляя (13.12) в (13.10), получим

[к,] =

1К1 =

5 EI Jdx

(13 13)

(13 14) (13.15)

Здесь матрица [k] - обычная матрица изгибной жесткости элемента. Матрица [kg] относится к эффектам упругой потери устойчивости и характеризует приращение изгибной жесткости. Поэтому ее часто называют инкрементальной матрицей жесткости. Как может быть установлено на основании выражения (13.15) и проверено в дальнейшем при выводе явного вида матрицы [к, отдельные члены этой матрицы зависят исключительно от геометрических параметров (например, длины). Поэтому эта матрица часто называется геометрической матрицей жесткости.

В случае изгиба потенциал прикладываемых нагрузок (узловых сил, см. рис. 13.1) задается выражением

= -LA/J{Fb (13.16)

поэтому вклад от изгиба в потенциальную энергию элемента равен

VV. = U + V =

[k/J{V}4-

[k,]{M-LA,J{Fb

(13.17)

При изгибе тонких пластин соотношения связи между перемещениями и деформациями, соответствующие (13.1), имеют вид (рис. 13.3)

(to \2

дх dw \2

(13.18)

дш dw dw

dxdu

дх ay

Проводя выкладки, полностью аналогичные приведенным выше, получим расширенный функционал энергии изгибных деформаций для изотропных пластин

D г dw ~ 2 J LV dx

dw , dwY , dw dw , nn J d V

dy / dx dy

dA +

(13.19)

где t - толщина пластины, a aJ, Oyi и ryt - интенсивности усилий в срединной плоскости (мембранные усилия), т. е. силы на единицу длины.

г, W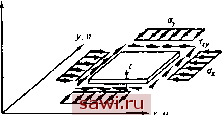

Рис. 13.3. Напряжения, действующие в срединной плоскости пластины при изгибе

Функциональное представление поперечных смещений можно опять записать в виде w= N J {А/}. При подстановке функции перемещений в (13.19) получим

-Ц [кП {A,f {АЛ-I-