деформации U*. Видно, что обе величины U н U* суть квадратичные функции параметров ( Д J и L J соответственно.

Как указывалось в разд. 2.3, всем возможным формам матрицы податливости для данного элемента отвечает одна и та же дополнительная энергия деформации. К примеру, рассмотрим вновь балочный элемент. Если балка свободно оперта (см. рис. 2.8(b)), то

2 -1 - 1 2

Чтобы сравнить с консольной балкой, вначале необходимо выразить силу Fi через моменты и М. Из условия равенства моментов относительно правой точки опоры (точки 2) получим Fi=-(Mj-f-+Мг)/1. Дополнительная энергия деформации для консольной балки имеет вид

&EI

2L 3L 3L 6

После подстановки полученного выше выражения для f i в формулу для и* и проведения выкладок приходим к выражению для U* в зависимости от Mi и М, полностью совпадающему с приведенным выше.

2.5. Свойства взаимности

Коэффициенты податливости и жесткости для линейно-упругого тела обладают свойством взаимности ifijfa и кц=кл). Этот факт имеет важное значение с точки зрения эффективности вычислительного процесса и может быть также полезен при проверке правиль-

Рис. 2 10.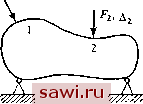

ности коэффициентов, получаемых численно или аналитически. Чтобы доказать теорему взаимности и тем са.мым определить пределы ее применимости и налагаемые при этом ограничения, рассмотрим выражения для работы, производимой над закрепленной конструкцией, изображенной на рис. 2.10, последовательно прикладываемыми нагрузками и fj. Обозначим указанную работу через

W. При постепенном приложении нагрузки Fi

W,=V (A,)xf,=V.(/ufi)fi. (2.5)

где нижний индекс у IF, и справа от круглых скобок, содержащих Аь означает соответствие силе 1. Прикладывая теперь Fa и оставляя неизменной F, с использованием аналогичных обозначений получим

W,~4,{A,UF,+iA,UF,4,(f F,)F,+(f,F,)Fu (2.6) поэтому полная работа Wi равна

r, = r + r,=V,/u(fi)+V,,(f,) +/i,f,f.. (2.7)

Меняя теперь порядок приложения сил и вновь подсчитывая вклад каждого слагаемого в работу, получим для нагружения силой f, (работу для указанной последовательности нагружений обозначим через 1F )

Wu=.hF,=4J {F,Y (2.5а)

и для прикладываемой вслед за этим силы Fi

W,=У,(,)гF + (,)гF,=УJn(Fгr+fnFгFг, (2.6а)

так что

W =tt .+ W =4J {F,r+y,UF,y+f2iFiF,. (2.7а)

Так как для линейного упругого тела последовательность приложения нагрузок не влияет на величину производимой работы, можно приравнять полученные выражения для W и, сократив подобные члены, получим

/ =/12. (2.8)

В общем случае будем иметь

fij4n- (2.9)

Это утверждение известно как теорема взаимности Максвелла.

Так как матрица, обратная симметричной матрице, также симметрична, а матрица жесткости является обратной к матрице податливости, то имеем

kijku. (2.10)

Теорема взаимности Максвелла обычно устанавливается как специальный случай закона Бетти, который гласит, что работа, производимая системой нагрузок {Pi} на перемещениях {Аа}, вызванных системой нагрузок {Р}, равна работе, производимой системой сил {Pj} на перемещениях {Ai}, вызванных силами {Pi}.

2.6. Преобразование соотношений жесткости и податливости

Имея для элемента один тип соотношений между силами и перемещениями, можно получить другие типы соотношений с помощью простых операций. Рассмотрим сначала преобразование соотношений жесткости в соотношения податливости. Проиллюстрируем этот случай на примере плоского элемента, изображенного на

У, V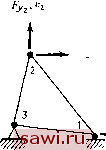

х, и

Рнс. 2.11. Плоский элемент, (а) Незакрепленный; (Ь) закрепленный.

рис. 2.П (а). Как указано в разд. 2.3, при построении соотношений податливости элемент должен быть закреплен таким образом, чтобы исключить движение его как твердого целого, и система должна быть статически определима. Указанный способ закрепления элемента изображен на рис. 2.П(Ь).

Величины, отвечающие закреплению, обозначаются нижним индексом S, а величины, соответствующие оставшимся степеням свободы,- нижним индексом /.

Итак, разбиваем матрицу жесткости следующим образом:

(2.11)

где для случая, изображенного на рис. 2.11(b), каждая из подматриц ([к ] и т. д.) является (ЗхЗ)-матрицей и

{А/} = L i 2 J {s) = L 3 щ щ J

Так как из-за условий закрепления {А,}=0, то

(2.12)

(2.13)