жесткости [к ]. Имеем

lkl + co[kgl{w}=0,

(13.29)

[ку]=[Г 1Т[ку][Г ], Гкг]=[Г 1Т[к,1[Г ]. (13.29а, Ь)

Собственное значение со и соответствующая форма моды выпучивания выделяются из редуцированной системы (13.29). Вопросы эффективности этой схемы будут описаны в дальнейшем.

13.3. Призматический элемент 13.3.1. Выпучивание при изгибе

Целью настоящих рассмотрений является преобразование энергии деформации (13.13) в явную формулировку для матрицы жесткости элемента посредством выбора функционального представления для W.

Точное представление для этого случая можно сформулировать, используя функцию перемещений, которая удовлетворяет соответствующему дифференциальному уравнению [13.1]. Однако, стремясь, как обычно, при конечно-элементном анализе выбрать простое аппроксимирующее поле перемещений, альтернативно выберем (при \=xlL) поле перемещений для изгибаемого элемента без осевой нагрузки (см. (5.14а)). Имеем

Использование выписанного выражения в (13.13) приводит к хорошо известному представлению для базисной изгибной матрицы [ку], задаваемой выражением (5.17), а также к следующей явной форме для матрицы [к]:

01 0.

[ г] - 30L

Г 36: -36 36 -3L 3L

(Симметрично)

-3L 3L -LML

(13.30)

В качестве примера применения инкрементальной матрицы жесткости при решении задач о потере устойчивости балок найдем критическую силу для изображенной на рис. 13.4 простой балки, используя один элемент. Здесь Wi = q2~0, Fx=-Рх, L = U2. По-

этому характеристическое уравнение примет вид

96£/

12Р,

/24е/

1 =0 10 J

решая которое получаем Px=9.94Ef/l. Это решение лишь на 0.752 /о отличается от точного решения л\Е1/1).

Рис. 13.4,

Отклонение

На рис. 13.5 представлена ошибка в процентах при решении этой задачи как функция от числа элементов разбиения. Для сравнения приведены соответствующие результаты для конечно-разностного решения [13.2]. Пониженная точность конечно-разностного решения вызвана допущением линейного изменения w между узлами по сравнению с принимаемым здесь кубическим характером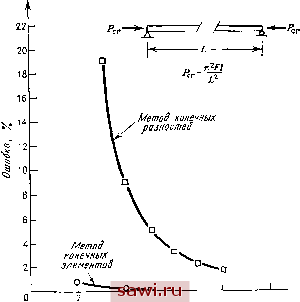

4 6

Число элементов

Рис. 13.5. Характеристики сходимости методов - выпучивание колонны Эйлера. 14*

изменения. Заметим, однако, что конечно-разностные уравнения используют только одну степень свободы в каждом узле, а именно прогиб W.

На рис. 13.6 изображен рафик зависимости ошибки в процентах от числа элементов в представлении при определении критической нагрузки суживающейся консольной балки. Сплошной линией

Сечение А-А Реошый

конструктидный элемент.-

л Ступенчатое предстабление

ШЭ-решение с нонрсоодразными с=0.25£ элементами v/= 0.50

-у Число КГ элементов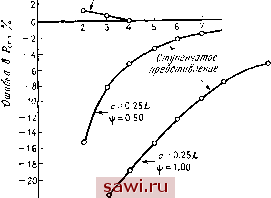

Рис. 13.6. Характеристики сходимости методов - устойчивость сужающейся балки

изображен график для ступенчатого представления [13.31, в котором для задания элемента используются геометрические характеристики в центре элемента. Следует отметить два аспекта, касающиеся полученных решений. Во-первых, точность решений при любой мелкости сетки строго меньше, чем для балки постоянного сечения. Во-вторых, решения для ступенчатого разбиения сходятся к точному решению снизу в отличие от решений для суживающихся элементов. Таким образом, становится очевидным, что более гибкая