геометрическая аппроксимация оказывается более важной по сравнению с аппроксимацией в конечно-элементном представлении функции перемещений. Более того, оказывается, что не существует представительного поперечного сечения элемента.

Трудно, а подчас и невозможно сформулировать точную матрицу жесткости для элемента с переменным поперечным сечением. С другой стороны, можно использовать принцип минимума потенциальной энергии при формулировке приближенного суживающегося элемента, задавая при этом геометрические характеристики, точно (как это сделано в разд. 6.4 и 7.2) или близко аппроксимируя форму суживающегося элемента и выбирая то представление перемещений, которое использовалось для элемента с постоянным поперечным сечением.

При применении этого подхода, сохраняющего непрерывность геометрических характеристик в узлах, получаются решения высокой точности, представленные на рис. 13.6 пунктирной линией. Пожалуй, наиболее важным заключением, вытекающим из проведенных рассмотрений, является то, что следует уделять большее внимание представлению геометрических характеристик по сравнению с выбором предполагаемых функций перемещений.

13.3.2. Изгибно-крутильная потеря устойчивости

Если призматический конструктивный элемент является частью пространственной стержневой системы, он, вообще говоря, подвергается изгибу в двух плоскостях, кручению вокруг своей оси и действию осевых нагрузок. Взаимодействие этих компонент порождает более сложные моды упругой потери устойчивости, нежели простые моды выпучивания, описанные в предыдущих разделах. Обобщение на этот случай осуществляется стандартными методами, не выходящими за рамки проведенных рассмотрений, и детально описывается в [13.4]. Чтобы проиллюстрировать используемые при этом операции, рассмотрим один из аспектов общего случая - условие из-гибно-крутильной формы потери устойчивости.

Призматический элемент, используемый при рассмотрениях, изображен на рис. 13.7. Предполагается, что для определения состояния элемента при изгибе и осевом деформировании в плоскости у - 2 до наступления выпучивания проводится независимый анализ. Таким образом, известны относительные амплитуды моментов на концах и М,;, перерезывающие силы в граничных точках fj Рг, и осевая нагрузка Fy. Рассматриваемая форма потери устойчивости включает кручение вокруг оси у и изгиб в плоскости X - у. Чтобы учесть депланацию, необходимо включить в качестве меры смещения производную от угла закрутки 0 по координате у, которую обозначим через 9 . Таким образом, для каждого конца элемента в качестве степеней свободы принимаются 6у, 6, и и

u(=du/dy) С соответствующими силовыми параметрами, обозначенными через My, Муу, и М.

При выписанных условиях для изгибно-крутильной формы потери устойчивости в [13.4] показано, что соответствующее выражение для потенциальной энергии имеет вид

ElAu r + GJ(Q,r + Er (%Г--(9;- ( +

+ (f+ iL-y) + Mx-Mj QX J dy-1=1

(13.31)

где штрихами обозначены производные по осевой координате у, G - модуль сдвига, J - жесткость кручения по Сен-Венану, /р - полярный момент инерции, Г - константа депланации, а величины А, Ii определены ранее; Мх =Мх-М.

Ух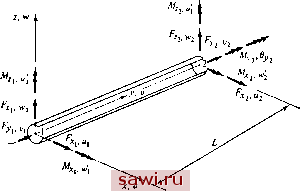

Рис, 13.7. Призматический элемент для анализа изгибно-крутильной формы потери устойчивости

Каждая из величин, характеризующих перемещения и и 9 , должна удовлетворять двум граничным условиям в каждом узле. Первое условие накладывается на сами переменные ut, Qy., а второе- на их первые производные и}, 9J. Этот тип условий встречался при простом изгибе. Поэтому в данном случае можно использовать представление функции в том же виде, как и для простого изгиба. Имеем

и = LN J{Au}. (13.32)

0 =LNJ{Ao }. (13.33)

F] .[[к,М1к,)]{л

{ } - ly Ii fy

- 3fi,i

1-1

+ 3F. t

+ 3F t

+ 3/vi

(CuMMempuf/fo)

2 t

t6F t

+ 3F i

Рис. 13.8. Матрицы жесткости для крутильно-изгибной потери устойчивости призматического элемента.