где L N J - вектор функций формы из (5.14а) и

(13.34) (13,35)

Подставив эти выражения в (13.31) и проведя интегрирование с применением принципа стационарности потенциальной энергии,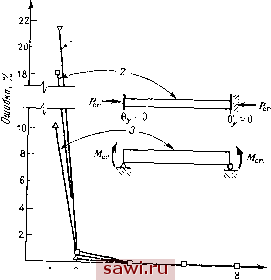

Voc/ro элементов

Рис. 13.9. Характеристики сходимости метода: изгибная (Л, крутильная (2) и поперечная (3) формы потери устойчивости.

Т. е. дифференцирования по каждой степени свободы в узле, приходим к уравнению жесткости того же вида, что и в предыдущих разделах данной главы:

{F}=[[M+[kJ]{A},

где в данном случае

Основная Ik] и геометрическая матрицы жесткости для этого случая изображены на рис. 13.8.

Чтобы проиллюстрировать точность формулировки, рассмотрим задачу о поперечной неустойчивости свободно опертой балки, концы которой не могут проворачиваться (рис. 13.9) при действии на

нее в этих точках одинаковых моментов Мх=-Мх=М,. Все остальные узловые параметры перемещений (щ, а, 6 QJ равны нулю. Применяя эти условия к уравнениям жесткости, представленным на рис. 13.8, получим

2Е1г

Z. W / 5 , 2£Т

= 0.

откуда имеем

.=А/ (EI,)(GJ)[ +

ЕГ 16

В этом случае точное решение равно

Если крутильная жесткость по Сен-Венану мала по сравнению с депланационной жесткостью (т. е. GJ<ET), ошибка достигает примерно 20%; если справедливо обратное, то для прямоугольного сечения ошибка приблизительно равна 10%.

На рис. 13.9 представлены данные по сходимости решений в случае крутильной и поперечной форм потери устойчивости, полученные с помощью выписанных формулировок. Для сравнения приведены результаты для ранее рассмотренного случая изгибной формы потери устойчивости. Во всех трех случаях при двухэлементной идеализации ошибка составляет менее 1 %.

13.3.3. Устойчивость стержневых систем

Анализ устойчивости стержневых систем представляет собой более сложную задачу, нежели одномерный (например, для балки) анализ устойчивости, так как распределение осевых нагрузок, вообще говоря, зависит от связанного изгибного и осевого деформирований конструкции. Поэтому задача устойчивости ие может быть сформулирована независимо от анализа осевого деформирования конструкции, что делает проблему нелинейной. Проиллюстрируем это утверждение на простом примере. На рис. 13.10 изображен узел / с силами (и перемещениями), прикладываемыми к элементу и отнесенными к локальной (для элемента) системе координат. Эти величины помечены штрихами. Для каждого элемента поэтому в линейном анализе устойчивости имеем

О !0

.0 ikgj

(13.36)

где делается различие между матрицами [kj и [к], характеризующими осевое и изгибное деформирования, а штрихи обозначают, ч-о этн матрицы относятся к осям, связанным с элементом После перехода к глобальным (без штрихов) координатам и н w соотношение между матрицами запишется в следующем виде

к к к к

(13 37)

Видно, что описание осевого и изгибного поведения является связанным, и члены, отвечающие линейной теории устойчивости, уже не отмечаются нижним индексом Это условие сохраняется после того, как все элементы объединяются при построении уравнений

7-* f

-Fx.4

Л/, 9

Рис. 13.10 Стержневой элемент - узловые силы (а) Локальные координаты, (Ь) глобальные координаты

ДЛЯ всей конструкции Таким образом, коэффициенты геометрической матрицы жесткости зависят от изгибного поведения конструкции и не могут быть определены независимо.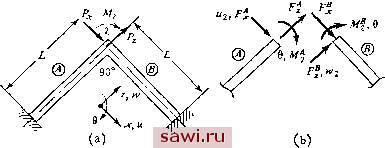

Рис 13 П. Пример простой рамы для анализа потери устойчивости (а) Рама, (Ь) конечно элементное представление

Чтобы проилаюстрировать эту ситуацию, рассмотрим раму, изображенную на рис 13 11(a) На рис 13 11(b) показана конечно-элементная идеализация этой рамы Только точка 2 может перемещаться, поэтому уравнение жесткости необходимо выписать лишь