ДЛЯ ЭТОЙ ТОЧКИ. С учетом базисных уравнений жесткости для поперечного и пpoдoьнoгo нагружения искомые выражения примут

10 R

6 L + 6 Z,

u.+LFB,

-w + LFfe

Заметим, что оси элементов соответствуют глобальным осям координат, поэтому штрихи, отличающие координатные системы, писать не нужно. После объединения элементов результирующие соотношения между силами и перемещениями запишутся в форме

(Симметрично)

£7 Z.2

6 L

о

6 L

(Симметрично)

2£ 15

или в суммарном виде

Изучение этих уравнений показывает, что силы F§4 F, которые входят в матрицу Kg], являются функциями от перемещений и

и 9 Поэтому непосредственное решение этой системы невозможно, и необходимо применить итерационную процедуру, описываемую ниже.

Сначала необходимо положить нулю члены матрицы [Kg] и найти перемещения. Имеем

(Симметрично)

6EI \2

(¥)

(¥)

P. P.

где ¥ =(AEIL+nEIIL),

det =

Л£ , 12£/

f Л£ , 12£/ \

L3 ;

8£/

Это решение для Ui, kji и Э можно подставить в уравнение для элементов и получить решение для и ff на первой итерации Последние можно использовать в матрице [К] и получить улучшенное решение для и, и 0. Итерации повторяются до тех пор, пока не будет получено сходящееся решение.

/ = 1000 срунтоб

12 дюйма В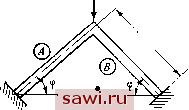

Рнс. 13.12. Рассчитываемая изменяемый угол в заделке

рама -

Поучительно сравнить решение, полученное на первой итерации при применении данного подхода, с решением, полученным при независимом определении осевых нагрузок. В последнем подходе Р=1000 фунтов, Р,=Л1г=0, f=0, ff = 1000 фунтов. С другой стороны, используя выписанные выше уравнения для первой итерации в случае L=12 дюймов и прямоугольного поперечного сечения 1 X 1 дюйм, получим =995.7.

Отличие приведенного выше решения от решения, в котором не учитывается взаимодействие осевых и изгибных деформаций, в этом случае невелико (примерно 0 5%). Однако для более детального изучения был проведен ряд расчетов для изображенной на рис. 13.12 конструкции с теми же характеристиками поперечного сечения и при различных значениях пологости или углового параметра ф. В табл. 13 1 приведены результаты, характеризующие увеличение точности (в процентах) в определении величин f=f, обусловленное учетом взаимодействия осевого и поперечного деформирования

по сравнению с упрощенным подходом. Очевидно, что взаимодействие изгибного и осевого деформирования может, вообще говоря, существенно влиять на потерю устойчивости упругих тел.

Влиянием прогибов на распределение осевых нагрузок обычно пренебрегают в так называемом классическом подходе к линейному анализу устойчивости. В этом случае вначале проводится анализ осевой нагрузки конструкции до изгиба. Далее строится непосредственно геометрическая матрица жесткости Однако трудно, а подчас невозможно использовать специальным образом высоко автоматизированные процедуры имеющихся в наличии вычислительных программ конечно-элементного анализа.

Примеры построения матриц для задач конечно-элементного анализа устойчивости стержневых систем можно найти в 113.5, 13.6].

13.4. Элементы для пластин

Набор элементов для изгиба пластин достаточно широк из-за разнообразия геометрических форм и полей перемещений, и для большей части жесткостные соотношения анализа упругой устойчивости слишком сложны, чтобы их приводить здесь. Построение подобных соотношений в явном виде для треугольных элементов особенно сложно. Поэтому ограничимся рассмотрением двух прямоугольных элементов. Читателю рекомендуется обратиться к работам 113.7- 13.12], где описаны подробности формулировки других изгибных пластинчатых элементов.

Двумя основными функциями перемещений для прямоугольного элемента являются двенадцатичленная (12 32) и шестнадцатичлен-ная полиномиальные функции, полученные при помощи полиномиальной эрмитовской интерпретации (12 31). Основное теоретическое соотношение для геометрических матриц жесткости элементов пластин задается выражением (13.21) (см. также комментарии к этой формуле). Подстановка двенадцатичленного полинома в эти уравне-