кости, связывающий F, и Oj (см. рис. 13.1), задается формулой EI ayL (\-шъшЦ L 2(1- COS (oZ.) -(oZ, sin ш1

где ш определяется так же, как и в задаче 13.3. Выпишите в полиномиальном виде этот коэффициент, разлагая в ряды тригонометрические функции, сохраняя два первых члена разложения. Сравните полученную формулировку с приведенной ь данной главе.

13.5, Рассчитайте свободно опертую балку-колонну, используя приведенную в этой главе матрицу [к], в случае действия центральной сосредоточенной силы Р и осевых нагрузок интенсивностью FjE.b, 0.75 и 0.9 [t={пЕЧU)]. Сраимите полученный результат с точным решением.

Рис. Р13.5.

13.6. Используя один элемент, вычислите критическую нагрузку для суживающейся балки, изображенной на рис. Р13.6.

/п. Аг,

Рис. Р13.6.

13.7. Расчлените уравнения анализа потери устойчивости по отношению к перемещениям {w} и (в), как это сделано в (13.28). Осуществите точную редукцию этих уравнений, разрешая нижнюю часть уравнений относительно (0). Далее, разлагая в ряд член [k--f cokJ , который фигурирует в результирующем

выражении, и исключая члены более высокого порядка, чем ш, покажите, что получаемое выражение совпадает с (13.29).

13.8. Для рамы, изображенной на рис. Р13.8, вычислите Р без учета осевой

Рис. Р13.8. (Размеры в футах.)

жесткости при построении соотношений связи ыежд} силами и перемещениями (Ясг=0.)35; £ из [13.15]).

13.9. Вычислите Р, для ступенчатой балкн, изображенной на рис Р13.9.

0.5/п

Рис. Р13.9.

13.10. Вычислите Рг для балки, изображенной на рис. Р13.10.

Рис. Р13.10.

13.11. (Задача для вычисления на ЭВМ.) Вычислите Рг для балки, изображенной на рис. PI3.11 (£=30-Ю фунт/дюйм, / =10.0 дюйм =2.0 дюйм).

Т ж-

Рис. P13.ll. (Размеры в футах.)

0.51 о, 2Ао

2/о, 1.5.4Г

13.12. Вычислите критическую нагрузку для заостренной колонны, используя один элемент с жесткостным представлением, сформулированным на базе эрмитова полиномиального представления поперечных смещений пятого порядка. Для этого представления требуется знание следующих степеней свободы: w, dwldx=-Wx и <Pwldx=Wxx в каждом узле. При этом

Lw=(L-\OLV + 1 SLx -6x)wi - L (L*x- 6L-x + 8Lx*-Зх ) , +

+Viii- (Lx - 3LV + ЗLx - x)wx + (lOL4- -\5Lx* + 6x) -

- L {7Lx* - 4LV + 3x)w iZ.= (LV- 2Lx* + x) w,.

13.13. Сформулируйте матрицу жесткости [к] для треугольного изгибного пластинчатого элемента, изображенного на рис. Р13.13, при наложении постоянных напряжений Ох срединной поверхности. Построение матрицы жесткости элемента основано на квадратичной (шестичленной) функции для w (см. рис. 12.8Ь из гл. 12).

Z, w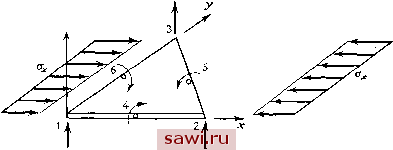

Рнс. Р13.13.

13.14. В кольцевом пластинчатом элементе, изображенном на рис. Р13.14, матрица жесткости которого построена в соответствующей задаче из гл. 12, значение температуры выросло на величину Г по сравнению с температурой для напряженного состояния. Используя один элемент, вычислите критическое значение Г, вызывающее выпучивание. (Используйте линейную по радиусу функцию смещения и линеаризуйте полученные в результате интегрирования выражения.)

Рис. PI3.14.

13.15. Для изображенной на рис. Р13.15 балки определите критическую нагрузку Р, используя два элемента. Сравните с точным решением n£ 4L.

Рис. Р13.15.

13.16. Для балки из задачи 13.15 определите зависимость основной частоты колебаний от следующих значений отношения приложенной нагрузки к эффективной критической силе : P=EliL, PjPct=W, PjPci=20, где L - длина элемента.