СПОСОБЫ ГЛОБАЛЬНОГО АНАЛИЗА КОНСТРУКЦИЙ

Существуют три основные группы методов построения алгебраических уравнений, отвечающих полному (глобальному) конечно-элементному представлению конструкций: методы перемещений (жесткости), методы сил (податливости) и смешанные методы. Вид этих уравнений аналогичен виду уравнений для элемента, определенных в разд. 2.3. Данные группы методов соответствуют различным формам энергетических принципов, и в дальнейшем будет удобно разрабатывать эти методы, опираясь на энергетические подходы. В данной главе изучаются два различных подхода к построению одного и того же типа глобальных уравнений, а именно уравнений жесткости, в которых роль неизвестных величин играют перемещения в узлах. Чтобы реализовать эти подходы, требуется лишь знание алгебраической формы записи матрицы жесткости конечного элемента и обозначений, введенных в разд. 2.3. Сами же подходы заключаются попросту в учете условий равновесия и непрерывности перемещений в узлах для полной аналитической конечно-элементной модели.

Цель указанных рассмотрений состоит в обеспечении читателя достаточными средствами для построения глобальных уравнений на основе соотношений для элементов, устанавливаемых в последующих главах, а не в тщательном обзоре возможных средств построения уравнений в методе конечных элементов. Жесткостные представления выбраны для описания потому, что, с точки зрения автора, это наиболее простые и эффективные из известных представлений. Кроме того, необходимо добавить, что использование жест-костных представлений налагает мало ограничений (или вообще не вносит ограничений) на характер задания конкретных уравнений для конечного элемента. Это объясняется тем, что, как показано в разд. 2.6, если уравнения выведены в одной форме (например, в форме уравнений податливости), то их можно преобразовать к другому виду (в данном примере возможно преобразование в уравнения жесткости).

3.1. Прямой метод жесткости. Основные понятия

Полный набор соотношений между силами и перемещениями для элемента с п степенями свободы, согласно (2.1), имеет вид

f, = + k,\, + ...+ Д +...+k

Л. (3.1)

Предполагается, что преобразование координат уже проведено, поэтому степени свободы отвечают глобальной системе координат конструкции. Числами l.../...л обозначены степени свободы в узлах элемента, и для рассматриваемого случая они соответствуют глобальной системе нумерации тех же узлов. В каждой строке уравнений (3.1) имеются все степени свободы. Способ крепления элемента не задан.

Как только соотношения между силами и перемещениями в элементе определены численно для каждого элемента конструкции,

Существует много различающихся деталями вариантов построения глобальной системы уравнений жесткости. Рассматриваемые в данной главе подходы - это прямые методы жесткости и методы конгруэнтных преобразований. Изложив эти методы, в разд. 3.4 задержимся для того, чтобы сделать обзор преимуществ (и некоторых ограничений) метода конечных элементов как общей процедуры расчета конструкций. В разд. 3.5 перейдем к изучению специальных операций над глобальными уравнениями, прн этом часть операций необходима, а часть полезна. Сюда входят разбиение на подконструкций, наложение ограничений и использование координат узлов.

В гл. 7 мы вернемся к вопросам расчета конструкции в целом, где уравнения жесткости будут изучены с других позиций. Кроме того, здесь же будут объяснены некоторые свойства решений, которые не могли быть объяснены прежде, а также изучены альтернативные формы глобальных уравнений (например, глобальные уравнения податливости). Так как в данном тексте основное внимание уделяется вопросам, связанным с построением элементов, то детальному описанию примеров глобальных уравнений отводится мало места. Читателю, интересующемуся подобными вопросами, следует обратиться к многочисленным книгам по матричным методам расчета конструкций (см., например, [3.1-3.4).

применение прямого метода жесткости заключается в объединении указанных соотношений в алгебраическом виде, как того требуют условия равновесия и совместности в узлах соединения элементов. Эти операции приводят к системе уравнений, связывающих силы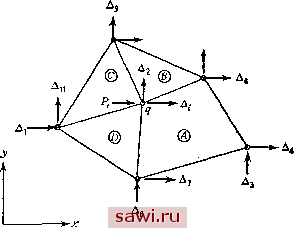

Рис. 3 1. Типичный узел внутри плоской конструкции.

г р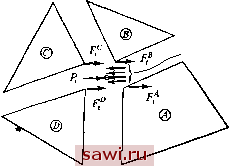

Рис. 3.2 Анализ равновесия в направлении Р,-Д/.

и перемещения в узловых точках элементов для конечно-элементной модели всей конструкции.

Чтобы проиллюстрировать эту методику, рассмотрим вывод уравнения связи между силами и перемещениями в точке q в направлении X для изображенной на рис. 3.1 аналитической конечно-элементной модели. Обозначим величины, отвечающие направлению х в точке q, нижним индексом i. Все изображенные элементы - три