* Для этого соединения следует обратить внимание на важную деталь обозначений Внутренние силы в узле (или силы в элементе) обозначаются символом F, а внешние силы в узле - через Р с соответствующими верхними и нижними индексами в каждом случае Здесь не вводятся отдельные символы для моментов в элементе и внешних моментов в угле, так как нигде в одной и той же задаче не будут фигурировать все величины сразу.

треугольника и четырехугольник - лежат в плоскости х - у. Для удобства на рис. 3.1 показаны степени свободы для всех узловых соединений, но только одна сила, представляющая внешнюю нагрузку Pt, которая действует в направлении х в точке д.

Согласно условиям равновесия в узле соединения, приложенная нагрузка Pt равна сумме внутренних сил, действующих в соответствующих элементах, прилежащих к узлу *К Чтобы пояснить это, покажем на рис. 3.2 элементы, прилежащие к рассматриваемому узлу. Из условия равновесия в направлении х имеем

PF+Ff+Ff+F?, (3.2)

где Ff - сила (внутренняя), действующая в направлении х в элементе А. Соотношения между напряжениями и смещениями для элементов, имеющие вид (3.1), приводят к выражениям для Ff, . . . . . . , Ff, записанным в терминах соответствующих степеней свободы элемента Af.....Aft. После подстановки указанных выражений в (3.2) приходим к соотношению

Pi={kfAf + kj,M +... + kfM) + (/гГ. A? + W + .

+ (kA?+k?A?+...+k?u?;}, (3.3)

a так как для A, В, С к D ъ силу условия совместности смещения Aj одни и те же для каждой степени свободы (A=Af =Af=Af= =Д,), то

Pi = {kfi + f, + ki + ЙЙ) A, + (kl -b Af) A, +

+ {kA+k.+k% + k?.)K+.. +(*f +*{,)A , (3.4)

или Pi=KiiAi-\-KiA\-\-KnAi+ ЛКтАхх. Это окончательная форма записи искомых уравнений. Обозначенные прописными буквами Ки, Ki\, Ktz.....Km величины суть глобальные коэффициенты жесткости, а уравнение (3.4) есть глобальное уравнение жесткости.

Важно отметить, что каждому из четырех элементов, которые соприкасаются в указанном узле соединения, отвечают коэффициенты жесткости с одинаковыми нижними индексами (например, kf, ku, ku, ki). Если нижние индексы для двух или нескольких различных элементов совпадают, то элементы имеют общую степень свободы, которая обозначается вторым нижним индексом. Тогда

3.2. Прямой метод жесткости. Общая методика

Для дальнейших построений предлагается следующий алгоритм получения уравнений, связывающих прикладываемые нагрузки и перемещения для всей конструкции

1. Перед вычислением каждому коэффициенту жесткости для элемента приписывается два нижних индекса (k ). Первый индекс i определяет силу, для которой записывается уравнение, а второй индекс / - соответствующую степень свободы.

2. Вводится массив (квадратная матрица), размерность которого равна числу степеней свободы всей системы с учетом того обстоятельства, что каждая сила связана соотношением с каждым перемещением системы. Каждый элемент массива обозначается двумя нижними индексами. Первый нижний индекс (строка) отвечает соответствующему уравнению для силы, второй индекс (столбец) - рассматриваемой степени свободы. В качестве иллюстрации на рис. 3.3 представлен массив, отвечающий двумерной конструкции с общим числом степеней свободы, равным п. Если встречается элемент, в обозначении которого имеется индекс 1, то он располагается в первой строке, в столбце с номером, равным второму нижнему индексу. Например, feia располагается, как указано на рис. 3.3(a).

3. Операции на шаге 2 выполняются для степени свободы с номером 1 до тех пор, пока все элементы не будут найдены. Каждый раз, когда коэффициент засылается в позицию с отличным от нуля значением, его значение прибавляется к последнему. После завершения операции на указанном шаге все элементы в первой строке достигают своего окончательного значения. Следовательно, для t-й степени свободы Ku = ku, где суммирование распространяется на все элементы, имеющие степень свободы /.

4. Операции, проведенные на шагах 2 и 3, повторяются для всех остальных степеней свободы В результате получают полный набор коэффициентов уравнений жесткости всей конструкции (глобальных уравнений жесткости), однако без учета условий закрепления.

5. Граничные условия учитываются, во-первых, выделением перемещений, равных нулю, с последующим устранением из уравнений коэффициентов жесткости, которые стоят сомножителями при указанных степенях свободы В результате получается больше

*> Распространенная альтернатива этой процедуры заключается в выделении с самого начала условий закрепления и построений матриц жесткости элементов только для незакрепленных степеней свободы. Тогда операции на шаге 2-4 приводят непосредственно к редуцированной матрице жесткости и ша1 5 исключается.

указанные коэффициенты складываются и получается один коэффициент в уравнении жесткости, которое отвечает силе, представленной первым нижним индексом.

уравнений, чем неизвестных. Дополнительные уравнения отвечают внешним нагрузкам в точках закрепления, т. е. реакциям опоры. Эти уравнения выделяются и хранятся для последующих преобразований.

(а) Ь

At Дг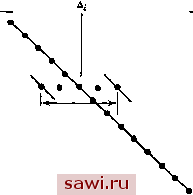

Ширина по/госы 61-й строке

Рис. 3.3. Основные аспекты задания глобальной матрицы жесткости, (а) Способ построения коэффициента /г,у в глобальной матрице жесткости и расположение коэффициента k, (Ь) типичный окончательный вид строки матрицы жесткости.

6. Образовавшаяся после выполнения операций на шаге 5 система уравнений решается относительно неизвестных степеней свободы. Внутренние силы, действующие в узлах элемента, определяются в результате подстановки найденных значений степеней свободы в соотношения, связывающие силы и перемещения в элементе. Нахождение указанных величин может потребовать преобразования глобальной системы координат в локальную систему координат с последующим вычислением напряжений.