Выполняемые в процессе реализации алгоритма алгебраические преобразования запишем в матричном виде. Предполагается, что операции на шаге 1-4 выполнены и глобальные уравнения жесткости выписаны и имеют вид

{Р}=[К1{А}. (3.5)

Далее предположим, что соответствующие закреплению степени свободы {As} можно сгруппировать, а уравнение (3.5) разбить на блоки так, чтобы выделить сгруппированные степени свободы (на практике эта операция не является необходимой и неудобна, но применяется здесь для большей ясности изложения). Итак,

Заметим, что нижние индексы вводятся в соответствии с разд. 2.6. Так как {Ag}=0, то

{Р,}=[К ]{А/}, {РЛ=[М{Д,}. (3.7а, Ь)

Общее решение уравнения (3.7а) получим в следующем символическом виде:

{Д,}=[К ]-ЧР/}=[Я{Р/}, (3.8)

где матрица IF] - совокупность глобальных коэффициентов влияния для перемещений. Подчеркнем, что операция обращения матрицы является символической. На практике, если рассматривается относительно небольшое число условий нагружения {Р}, наиболее эффективный способ реализации этого процесса состоит в решении указанных уравнений с известной правой частью.

Реакции опоры {Р) находятся в результате подстановки уравнения (3.8) в (3.7Ь):

{РЛ=[М[/=-1{Ру}. (3.7с)

Чтобы определить распределение внутренних сил в м элементе, можно подставить вычисленные степени свободы данного элемента, обозначаемые ниже через {Д}, в матрицу жесткости элемента [к], что приведет к вычислению усилий {F} в узлах соединения этого элемента. Чтобы получить напряжения, а не усилия в узлах, зная перемещения, необходимо перед выполнением расчета вывести обычные соотношения, связывающие напряжения в элементе с соответствующими значениями степеней свободы в узловых точках, а именно

{о} = 151{Д}, (3.9)

где {о} - величины напряжений, характеризующих напряженное состояние внутри i-ro элемента, а IS] - соответствующая матрица жесткости элемента. Вектор {о} объединяет величины напряжений в заданной точке элемента. Таким образом, при этом подходе, если вектор перемещений для элемента вычислен, то для определения напряжений необходимо умножить его слева на соответствующую матрицу жесткости.

В предыдущих рассмотрениях не было уделено внимание некоторым основным свойствам глобальных уравнений жесткости. Во-первых, свойство симметрии коэффициентов жесткости элементов обеспечивает симметричность коэффициентов глобальных уравнений жесткости, поэтому необходимо держать в памяти ЭВМ лишь диагональные элементы матрицы и элементы по одну сторону от диагонали. Во-вторых, как было указано, отвечающие данной степени свободы уравнения жесткости (уравнения равновесия) зависят от степеней свободы тех элементов, которые прилежат к узлу, где задана исходная степень свободы.

Изображенные на рис. 3.1 элементы могут представлять лишь небольшую часть реальной конечно-элементной модели. Элементы, которые находятся вне области, занимаемой элементами А, В, С и D, никак не влияют на вид уравнения (3.4). Другими словами, совокупность отличных от нуля элементов в строке матрицы жесткости состоит из коэффициента на главной диагонали и коэффициентов, отвечающих степеням свободы в данном узле и узлам элементов, которые прилежат к данному узлу. Все остальные элементы в строке равны нулю. Если в полной конечно-элементной модели существует много степеней свободы, а матрица жесткости содержит относительно мало нулевых элементов, то такая матрица называется разреженной или слабо заселенной матрицей.

Очевидно, что с вычислительной точки зрения удобно прижать все нулевые элементы как можно ближе к главной диагонали матрицы (см. рис. 3.3(b)), выделяя тем самым нулевые элементы и облегчая их исключение из вычислительного процесса. Это можно сделать, нумеруя степени свободы таким образом, чтобы расстояние от главной диагонали до самого удаленного нулевого элемента в каждой строке было наименьшим, т. е. минимизируя ширину полосы ленточной матрицы.

Минимизация ширины полосы ленточной матрицы - это всего лишь один из способов увеличения эффективности вычислительного алгоритма решения уравнений. Какой бы подход ни применялся для экономичности вычислительного процесса, существен учет свойств симметричности и разреженности матриц жесткости. Обсуждение алгоритмов численного решения уравнений лежит за пределами данной книги, поэтому читателю, желающему получить всестороннее представление о данном вопросе, рекомендуется обратиться к работам 13.5],

Все детали реализации изложенного выше прямого метода жесткости проиллюстрированы на рис. 3.4. Далее рассмотрен пример расчета подкрепленного треугольного элемента.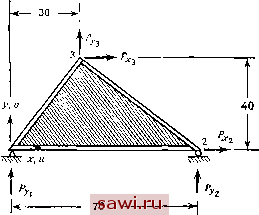

t t

А= 0.7S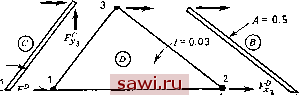

=0.7

Рис. 3.4. Иллюстративный пример - прямой метод жесткости, примененный к подкрепленному треугольному элементу (линейные размеры даны в дюймах, площадь А - в квадратных дюймах). Пример расчета см. ниже.

Пример расчета треугольного элемента (см. рис. 3.4)

Уравнение жесткости элемента. £=10 фунт/дюйм, ц=0.3. Все величины вычисляются вручную. Для элемента А (элемент 1-2) справедливо /4/L=0.7/70. Относительно матрицы жесткости см. разд. 2.3. Преобразование проводится согласно разд, 2.7; при этом со5ф=1, sin ф=0:

1.000 -1.000 -1.000 1.000