и поэтому матрица [А] содержит только единичные ненулевые элементы.

Развиваемый здесь на базе естественных рассуждений метод конгруэнтных преобразований можно также построить, используя энергетический принцип. Этот альтернативный подход излагается в разд. 7.2. Будет показано, что указанный альтернативный подход позволяет выявить особенности расчета всей конструкции без построения на практике глобальных матриц. Этот подход известен как процесс прямой минимизации энергии 13.6].

Прежде чем подвести итог данного раздела, рассмотрим некоторые важные свойства статической матрицы системы 1] (и, конечно, транспонированной матрицы - кинематической матрицы системы [А]). Это позволит выявить любую возможную форму кинематической неустойчивости конечно-элементной модели конструкции и определить дополнительные силы. Конструкция кинематически неустойчива, если при приложении рТГл впзн{сдрт формы движения как~абсолютно твердого тела. Дополнительные силы - это силы, переопределяющие статически определимую систему.

Чтобы описать действия, которые необходимо проделать над уравнениями статики для определения указанных выше величин, рассмотрим конечно-элементную модель плоской фермы, содержащую п степеней свободы (так как каждому узлу соответствует две степени свободы, то число узлов равно /г/2), р элементов и t опорных реакций. Обобщение на более сложные случаи не представляет труда.

Построим сначала вектор сил {F} таким образом, чтобы он содержал внутренние силы в элементах (т. е. составляющие, отвечающие движению тела как жесткого целого, исключаются), а также силы реакции опоры для всей конструкции. Этих сил достаточно, чтобы описать условия равновесия для единственного набора внешних нагрузок {Р}. Тогда для описания этих условий опять применимо уравнение (3.15). Перепишем (3.15) в следующем виде:

[:-П{р} = 0. (3.15а)

Матрицу 1В\-\] назовем дополнительной матрицей. Так как она составлена с учетом двух уравнений равновесия в каждом из п/2 узлов, то в ней п строк. Для р усилий в элементах и t реакций опор вектор {F} содержит (p+t) компонент, а для статически неопределимой конструкции это число превосходит п. Разность г= = {p+t)-n соответствует числу дополнительных сил. Основной задачей при выявлении дополнительных сил и (или) кинематической неустойчивости является выделение г компонент вектора {F}. Эти компоненты {F} и есть дополнительные силы (силы, статически переопределяющие систему). Далее выражаем оставшиеся ста-

{F } через дополнительные силы {F} и {Р}. Это можно осуществить, применяя

тически определимые силы прикладываемые нагрузки процедуру исключения Гаусса - Жордана.

Применение процедуры исключения Гаусса - Жордана для матрицы [В\-II заключается в следующем:

1. Все элементы первой строки дополнительной матрицы делятся на коэффициент, стоящий в первом столбце. (Если в первом столбце стоит нулевой элемент, то необходимо предварительно соответствующим образом поменять местами столбцы.)

2. После деления каждый элемент первой строки умножается на коэффициент, стоящий в первом столбце второй строки, и полученные значения вычитаются из соответствующих элементов второй строки. В результате получим модифицированную вторую строку, у которой в первом столбце стоит нулевой элемент. Аналогичные операции проделываются со всеми остальными строками, что приводит к обнулению всех элементов, кроме первого, стоящих в первом столбце.

3. Операции, выполняемые на шагах 1 и 2, повторяют для второго столбца, добиваясь обнуления всех элементов столбца, кроме элемента, стоящего на главной диагонали матрицы, значение которого получается равным единице. Эту операцию повторяют для каждого из столбцов, образуя в итоге единичную [11 матрицу порядка пХп.

В соответствии с изложенным выше уравнение (3.15а) преобразуется к виду

откуда

[1 С, 1С,] {F } = -[Q]{P}

= 0,

(3.15b) (3.15с)

Наконец, преобразуем это выражение таким образом, чтобы получить в левой части равенства ({F}= F* FJ)

{F} = [D,]{PK[,]{F},

(3.15d)

г-с,

......

Относительно изложенной процедуры сначала заметим, что соответствующие {F°} столбцы матрицы не обязательно должны быть первыми п столбцами исходной матрицы [fi;-1]. Поэтому выявление дополнительных сил можно осуществить при достаточно произвольном начальном выборе столбцов матрицы. Желательно до нормализации главного диагонального элемента отыскать столбец с наилучшим значением коэффициента в соответствующей строке. Найденный столбец следует поменять местами с вектором, занимающим исходный столбец, а затем выполнить нормализацию

И другие операции (шаг 2). Существует ряд соображений относительно критерия выбора наилучшего коэффициента в строке. Простейшим из них является выбор столбца с наибольшим значением коэффициента.

Второе замечание, касающееся вышеизложенной процедуры, заключается в том, что кинематическая неустойчивость конечно-элементной модели выявляетея по наличию нулевых строк, причем их число соответствует числу степеней свободы указанной неустойчивости. С помощью процедуры исключения Гаусса - Жордана формируются диагональные матрицы. Напомним, что, согласно разд., 2.9, в матрице жесткости элемента можно выявить степени свободы, отвечающие движению тела как твердого целого, если преобразовать матрицу жесткости к диагональному виду и выделить ее нулевые диагональные элементы. В настоящем рассмотрении ненулевые элементы диагональной матрицы состоят из коэффициентов всех независимых уравнений.

На рис. 3.7 иллюстрируются операции по определению кинематической неустойчивости простой фермовой конструкции с помощью вышеизложенной процедуры.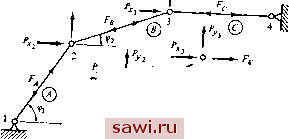

о FB ltumR S1/3/те 3

Рис. 3.7. Выявление кинематической неустойчивости с помощью процедуры исключения Гаусса-Жордана в уравнениях равновесия для узлов.

Чтобы упростить алгебраические выкладки, из расчета исключаются опорные точки 1 и 4, при этом уравнения равновесия в узлах 2 и 3 имеют следующий вид (Са=соь Фз, S2=sin фг и т. д.):