Нормализуя первую строку на элемент, стоящий в первом столбце (т. е. разделив элементы первой строки на -Cj), получим

1

Исключаем в первом столбце элемент, стоящий во второй строке, умножая элемент в первой строке на и складывая с элементом во второй строке. Кроме того, разделим образовавшиеся вторую и четвертую строки на Si, а третью - на с.

-С2/С1

(Sa/Si-Cj/Ci)

- Сг/Ci

- Sj/Sj

1/s, 0 0

1/Cl

0 0 0

1/s,

Исключим элемент, стоящий на пересечении второй строки и второго столбца, складывая с четвертой и вычитая третью строку из второй. Нормализуем на элемент, стоящий на пересечении четвертой строки и второго столбца (т. е. умножаем на -Sj/sj):

Г 1 О О О

- Cl/C,

- 1/Ci

- I/C1 О

- 1/Cl

- 1/ci

- I/C2 О

1/Si

- l/Sj

Исключим все остальные элементы во втором столбце, т. е. только элемент в третьей строке. Для этого умножим четвертую строку на -I и сложим с третьей строкой. Получим

-Ci/Cj

- 1/ci

- 1/Cs

I/S3 О

- 1/с,

- 1/с,

- I/C2 О

1/S, - 1/ 2 J

Нормализуем на элемент, стоящий на пересеч1нии третьей строки и третьего столбца (т. е. помножим на Cj/cj):

Исключим все элементы в третьем столбце, прибавляя к соответствующим стро-

Получена единичная матрица, отвечающая внутренним силам. Образовавшаяся нулевая строка указывает на кинематическую неустойчивость для одной из степеней свободы.

3.4. Обзор преимуществ метода конечных элементов

На рис. 3.8 отражена довольно общая ситуация, возникающая при расчете конструкций. Все аспекты этой гипотетической ситуации встречаются при проектировании реальных конструкций, описанных в гл. 1. Геометрию всей конструкции нельзя описать единым математическим выражением, а наличие вырезов и выделенных направ-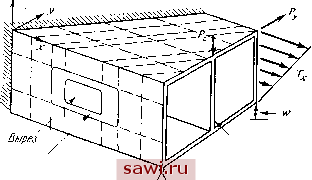

Подкрепляющая пластина

ПоЗнреп/1яюш,ая стойка

Рнс. 3.8 Общая ситуация, возникающая при проектировании конструкций (штриховыми линиями обозначены ребра жесткости); Тх- прикладываемые распределенные нагрузки; О) - задаваемые перемещения.

лений для ребер жесткости исключает возможность использования регулярной сетки разбиения. Различные условия закрепления, как силовые, так н кинематические, а также условия нагружения трудно учесть при расчетах классическими методами даже для конструкций с очень упрощенной конфигурацией. Указанные факторы, относящиеся к заданию аналитической модели, геометрии конструкции, а также граничных условий, для численного решения задач подобного типа вынуждают применить метод конечных элементов. К этим факторам, которые обсуждаются ниже, добавляется фактор представления свойств материала конструкции.

Наиболее очевидное преимущество конечно-элементного анализа, как отмечалось выше, заключается в представлении большого количества конструктивных элементов заданной аналитической моделью - пластин, трехмерных тел, ребер жесткости, частей оболочек и т. д. Таким образом, имеется широкая область аналитического представления. На практике, вообще говоря, существуют обстоятельства, ограничивающие указанные воз.можности. О некоторых из них речь пойдет в следующих главах. Так, например, для конечно-элементной модели пластины с ребром жесткости контакт пластины с ребром имеет место лишь в узловых точках. Поэтому для

обеспечения непрерывности механических характеристик конструкции (перемещений и напряжений) на линии, соединяющей указанные узловые точки, на конечно-элементные представления требуется наложить соответствующие ограничения. Вообще говоря, всем требованиям, обеспечивающим непрерывность характеристик при переходе от элемента к э;гементу, в полном объе.ме удовлетворить нельзя, поэтому большая доля теоретических исследований в методе конечных элементов посвящена рассмотрению указанных вопросов и выявлению требований, которые возникают при построении конечных элементов.

Другим сдерживающим фактором при построении конечно-элементной модели является выбор упрощенных функций для построения часто встречающихся элементов. В окрестности углов у вырезов в конструкциях возникает, например, концентрация напряжений. Поэтому в тех случаях, когда при проектировании существенно знание характера изменения поля напряжений, для описания этого поля необходимо значительное измельчение сетки разбиения. В противоположность аналитическим методам, требующим использования регулярных сеток, измельчение сетки здесь можно провести относительно просто, но, чтобы это усовершенствование было экономически оправданным, нужно, чтобы оно было соразмерно требуемой точности решения.

В описанных выше случаях можно ввести специальные конечные элементы, которые построены с использованием более сложных функций, описывающих резкое изменение напряжений. Подобное поведение имеет место вблизи границ конструкций, в областях приложения сосредоточенных нагрузок. Здесь также существует альтернатива выбора: измельчение сетки с простыми элементами или задание специальных элементов на грубой сетке.

Одним из особых преимуществ мето; конечных элементов, давно выделенным специалистами, является возможность геометрического представления конструкции, т. е. задание используемой при расчете сетки разбиения существенно нерегулярным способом. Мы уже столкнулись с идеей введения в плоских задачах треугольных элементов, а в гл. 5 и далее будут выведены соотношения между перемещениями и силами для этих элементов. Универсальность задания сетки разбиения с помощью треугольных элементов совершенно очевидна. Весьма существенны, хотя и менее явно выражены, преимущества от представления сетки разбиения криволинейными элементами. В разд. 8.8 рассматривается частный случай, когда граничные кривые определяются полиномиальными выражениями. Этот случай задания сетки называется изопараметричестм.

Граничные условия как для сил (прикладываемых усилий), так и для перемещений учитываются весьма легко с помощью рассмотрений, изложенных в предыдущих разделах. Ранее подразумевалось, что прикладываемые силы имели сосредоточенный характер.