{АЛ = [Го] {АЛ. (3.27)

Применяя это соотношение к равенству (3.20), получим (3.25).

Более эффективным подходом к расчету сложных конструкций может служить метод редуцированных подконструкции [3.11]. Чтобы аналитически описать этот подход, необходимо усилить концепцию уравнений связи, которая принимается в п. 3.5.2.

3.5.2. Уравнения связи

Уравнения связи - это соотношения между степенями свободы, задаваемые дополнительно к основным уравнениям жесткости. Простое задание условий закрепления, т. е. А;=0, приводит к ограничениям, но, как было видно, его легко учесть непосредственно после построения глобальной матрицы жесткости. Целям настоящих рассмотрений более соответствует показанный на рис. 3.10 случай изгибаемого элемента, соединенного с твердым телом. Ясно, что на смещение узлов 1-5 наложены связи, препятствующие установлению линейного закона для смещения ш, которое диктуется угловым смещением нормали к срединной поверхности оболочечного элемента. Связи возникают и во многих других случаях, включая обсуждаемую в следующем разделе схему метода редуцированных подконструкции, некоторые подходы к расчету не-

Полученное уравнение жесткости в совокупности с аналогичными уравнениями для других основных подконструкции можно использовать при построении уравнений жесткости для степеней свободы, отвечающих участкам соприкосновения подконструкции, т. е. для всей конструкции (подконструкции F, G а Н):

{Pc}={Fn+{FO}+{F }, (3.26)

где верхними индексами F, G и Н помечены соответствующие силы на участках соприкосновения.

Решая полученные уравнения, находим перемещения на участках соприкосновения {А}. Чтобы получить силы и перемещения внутри подконструкции, перемещения (А} подставляются снова в уравнения для подконструкции (3.20) и (3.21).

Требуемый процесс конденсации можно осуществить также с помощью преобразования координат. Вспоминая, что, согласно разд. 2.8, если совокупность степеней свободы сопоставляется с меньшим числом степеней свободы с помощью матрицы преобразования [Го], то исходная матрица жесткости преобразуется с помощью тройного произведения [Го] [К] [Го1, а вектор сил преобразуется согласно [Го] {Р} (см. уравнения (2.37) и (2.38)). В данном случае в силу (3.21) и с учетом равенства {А}=[1] {А} получим

сжимаемых материалов, а также при учете специальных граничных условий и при попытках задать определенные типы перемещений на некоторых участках конструкции. Далее в книге встретятся указанные ситуации.

iZ, И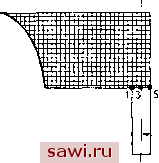

твердое у тело

Оболочечный элемент

Рис. 3.10. Изгибаемый оболочечный элемент, соединенный с твердым телом.

Каждое уравнение связи позволяет исключить одну из степеней свободы, оставляя другие. Используем здесь эту возможность для построения матрицы преобразования, которую можно применять для конденсации стольких степеней свободы, сколько ограничений задано сверх числа уравнений жесткости. Таким образом, используем подход, предложенный в разд. 2.8.

Рассмотрим случай, когда имеется г связей в системе с п степенями свободы. Общее представление линейных уравнений связи- в этом случае и.меет вид

lGlrxn{A}r,Xl={s}rxl,

(3.28)

где элементы в [GI суть коэффициенты в уравнениях, задающих ограничения, а {s} - вектор, компоненты которого заданные константы. Для простоты рассмотрим лишь случай {s}=0. Вывод соотношений для более общего случая {s}=7>0 представляется сделать читателю в качестве упражнения (см. задачу 3.]8).

Для построения матрицы преобразования вновь проведем разбиение степеней свободы на две группы {Л} и {Д}, где {А} содержит г степеней свободы, а {А} содержит (п-г) степеней свободы. Имеем

]{л;}=0- (3.29)

Таким образом, степени свободы объединены так, что {А} степеней выбраны в соответствии с числом ограничений г. Требуется исключить эти степени свободы из выражения для функционала энергии посредством схемы конденсации. Хотя выбор исключаемых степеней

свободы часто произволен, возникают случаи, когда это необходимо делать с чрезвычайными предосторожностями [3.12]. Разрешая (3.29) относительно {А}, получим

{A,}=-[GJ- [GJ {A,}=[GJ {АЛ, (3.30)

что, согласно схеме, разработанной в разд. 2.8, можно использовать для получения формул преобразования степеней свободы в следующем виде:

{::Ь[

.....

{АЛ = [ГЛ{АЛ.

(3.31)

Применяя полученные формулы к глобальным уравнениям в виде тройного произведения [Г1 [к] [Г], получаем редуцированную матрицу жесткости, относящуюся только к {А}, а также редуцированный вектор сил

-гг пт

Решая редуцированные уравнения жесткости, находим {А}, который можно подставить в (3.30) и найти {А}.

Рис. 3.11.

В качестве иллюстрации рассмотрим изображенную на рис. 3.11 систему, состоящую из трех стержневых элементов. Согласно прямому методу жесткости, система уравнений без учета условий закреплений имеет вид (ko=AE/L)

г 1

- 1 2 (Симметрично) 0-1 2

L О О -1 1 J

а с учетом условий закрепления Ui=u=0 записывается как

2 -1

Предположим теперь, что узлы 2 и 3 жестко соединены таким образом, что Ui=U3. В матричной форме это записывается в виде