Поэтому формулы преобразования имеют вид

а редуцированные уравнения жесткости переходят в уравнения

2 -Г

feo L 11 J

или 2йо з=Я2+Рз. Этот ответ согласуется с очевидным решением данной задачи. Ограничения преобразуют элемент В в жесткую связь между узлами 2 и 3. Поэтому приложенная нагрузка равна сумме усилий в этих узлах (Рг+Рз), а коэффициент при и, равен сумме жесткостей элементов Л и С, которые по существу соединены в одном и том же узле.

Рис. 3 12.

Следует отметить, что во многих случаях лишь часть из полного набора степеней свободы может фигурировать в уравнениях связи. На рис. 3.12, например, величины и не появляются в уравнениях связи только в том случае, когда , и з взаимосвязаны. Предположим теперь, что полный набор степеней свободы можно представить как LA J = L LJ LA J LAg J J, где группы LAJ и [ AJ фигурируют в уравнениях связи, аналогичных (3.29), а набор [ AgJ не фигурирует в них. Тогда можно записать следующее преобразование степеней свободы:

(3.32)

где irj определяется согласно (3.31). Это преобразование можно применить непосредственно к глобальным уравнениям жесткости обычны.м образом.

Если связи накладываются на относительно небольшое число степеней свободы, может оказаться более эффективным включение связей в глобальную матрицу жесткости на основе непосредственных выкладок по сравнению с использованием для этого матричного преобразования. Прямой метод аналогичен подходу, применяемому для специальной системы координат в п. 3.5.3.

Вернемся теперь к схеме редуцированных подконструкций, в которой операции конденсации и наложения связей включены в

единую матрицу преобразований. Предположим, что граничные узлы разделены на две группы. Так же как и прежде, степени свободы {А} приписываются соседним подконструкциям. На перемещения, отвечающие оставшимся граничным степеням свободы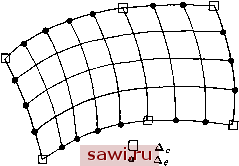

Рис. 3.13. Схема анализа с помощью редуцированных подконструкции

{Ag}, наложены связи, вид которых определяется степенями свободы {А} (рис. 3.13). Перемещения, отвечающие степеням свободы {А}, могут задаваться, например, в виде линейной, квадратичной или другой, имеющей более высокий порядок функции. Разбивая матрицу жесткости подконструкции на клетки, получим

Определим также, аналогично (3.30), соотношения между {А} и {Ар}, которые задают ограничения, т. е. {А} = [01 {А}. Вспоминаем далее, что, согласно разд. 2 8, искомая матрица преобразований строится в результате приравнивания нулю сил, соответствующих исключаемым степеням свободы. Поэтому, решая верхние уравнения относительно {А;} при {f(i}=0, получим

{Arf}=-[kdJ-4[kJ {A,}+[kJ {АЛ1. (3.34)

Подставляя в эту формулу выражение (3.30), приходим к уравнению

{A,} -Ik,J-4[k,J[G,J+[k,]] {АЛ- (3.35)

Комбинируя соотношения (3.30), (3.35) и учитывая, что {АЛ = = [1] {А}, запишем окончательно искомое преобразование в виде

Arf А.

-М-Ч[к..][0,Л + [к</.]]

{АЛ = [Г] {АЛ. (3.36)

4 Xs 25 47

Эти соотношения можно применить к уравнению (3.33) в внде преобразования, чтобы получить матрицу жесткости, относящуюся лишь к {Л} и соответствующему редуцированному вектору сил.

Проиллюстрируем этот подход, обращаясь к рис. 3.14, где изображена конструкция, состоящая из четырех плоских прямоугольных элементов, каждый из которых построен в предположении о линейности смещений на границе элемента (подробности см. в гл. 9;

Рис. 3.14.

там же приведена матрица жесткости элемента). Предположим, что на границе конструкции смещения изменяются по линейному закону. Тогда величины и, Ua, u, и, v, Va, и представляют степени свободы {A}, а u, u Ug, u v y v, v- степени свободы {A}. Внутренние степени свободы суть Ui и Vi, поэтому {А}= = \ UiV-i, \. Ниже в соответствии с(3.30)для этой задачи построена матрица [G], остальные матрицы ([kdi, [kdj, IkdJ). которые необходимы для построения матрицы преобразования из (3.36), определяются с помощью матрицы жесткости всей конструкции. Интересно заметить, что матрица жесткости, получаемая в результате этого преобразования и имеющая отношение только к угловым узлам, идентична матрице, получаемой в том случае, когда вся область представляется в виде одного элемента с линейным законом изменения перемещений на контуре и с использованием матрицы жесткости элемента, приведенной на рис. 9.13.

{АЛ =

= [GJ{A,}.