3.5.3. Связанная система координат

Иногда бывает необходимо записать часть глобальных уравнений в связанной системе координат, особенно в тех случаях, когда условия закрепления задаются вдоль направлений, отличных от направления осей глобальной системы координат, или когда оболочка рассчитывается с помощью плоских пластинчатых элементов.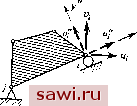

PuHmueHaRjjtoffTi, npi/жина

-X, и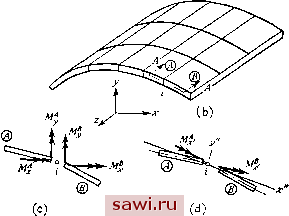

Рис. 3.15. Локальные координаты в конечно-элементном анализе, (а) Закрепление, ограничивающее вращение, и оси координат; (Ь) конечно-элементное представление оболочечной конструкции; (с) векторы мо.чентов в глобальной системе координат; (d) векторы моментов в локальной системе координат.

Типичная ситуация представлена на рис. 3.15(a). Смещение точки i описывается компонентами смещения и; и Uj в глобальной системе. Однако простое приравнивание нулю одной или обеих компонент не будет правильно представлять связь, накладываемую условиями закрепления в направлении у . Связи можно задавать корректно, если выразить поведение точки i в терминах компонент смещений lii и vl в системе координат, помеченной двумя штрихами, после чего Uj полагают равной нулю.

На рис. 3.15(b) изображена оболочечная конструкция, которая моделируется в виде системы плоских пластинчатых конечных элементов. На рис. 3.15(c) и (d) в векторном виде отражены условия равновесия для моментов в узле i для сечения А - Л. Из рнс. 3.15(c) следует, что в глобальной системе координат существенны составляющие векторов в обоих направлениях х а у. Однако, согласно рис. 3.15(d), на котором изображены векторы моментов М в осях элементов, а также связанная система координат х -у (ось х которой направлена по касательной к оболочке в точке i), очевидно, что проекции векторов на ось у малы по сравнению с проекциями на ось х . Вообще говоря, в реальной конструкции составляющая вдоль оси у равна нулю. Указанная диспропорция компонент в ортогональных направлениях приводит к серьезным последствиям прн решении глобальных уравнений. Один из способов избавиться от этих последствий состоит в том, чтобы в каждом узле ввести связанную систему координат х -у и исключить малые составляющие вдоль оси у , как если бы это были закрепленные степени свободы.

На примере задачи, представленной на рис. 3.15(a), опишем подробнее, каким образом преобразуется глобальная матрица жесткости, чтобы она соответствовала системе координат, связанной с узлами. Для заданных координат узлов i и j направляющие косинусы осей системы координат х -у вычисляются в виде 1х= - {Xi-Xj)IL, 1у={У1-yi)IL по отношению к осям системы координат х-у, где L=У{х~х-)+{yi~yj)\

Теперь, используя полученные направляющие косинусы, проекции смещения ui и и} можно выразить через проекции смещения Ui и Vi следующим образом (см. разд. 2.7, где приведен указанный вид преобразования):

uilu-lyVi, (3.37)

vi==lyU; + lVi. (3.38)

Для глобальной матрицы жесткости это значит, что столбец исходной глобальной матрицы жесткости, умноженный на следует умножить на 4 и вычесть из произведения 1у на столбец, умноженный на Vi. Полученный вектор-столбец, соответствующий заменяет вектор-столбец, соответствующий Ui. Эта операция проиллюстрирована на рис. 3.16. Аналогичная операция, отвечающая (3.38) и заменяющая у,- на vl, также представлена на рис. 3.16.

Силовые равенства (строки) в глобальных уравнениях жесткости преобразуются на базе аналогичных рассуждений. Так, согласно обычному преобразованию координат, имеем

P.f-P, + /y, (3.39)

= + (3-40)

Согласно ЭТИМ уравнениям, новая строка, стоящая на месте f , строится путем умножения на строки, соответствующей F и умножения на 1у строки, соответствующей F., и последующего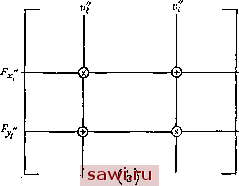

Рис. 3.16. Лодифицированная 1Лобальная матрица жесткости, (а) Исходная глобальная матрица жесткости; (Ь) модифицированная глобальная матрица жесткости. Строка для Fx- получена суммированием умноженной на 1 строки для Fx/ II умноженной на ty строки для Fy.; строка для Fy получена суммированием умноженной на -1у строки для F и умноженной на / строки для Fy; столбец для получен суммированием умноженного на 1 столбца для и умноженного на 1у столбца для V;; столбец для и получен суммированием умноженного на - столбца для ui и умноженною на 1 столбца для vi.

Замечание. Произведения коэффициентов при строках и столбцах на главных диагоналях (помечены символом х) и на перееечениях (-f) равны соответственно квадратам и произведениям величин 1 и /у.

сложения строк. Новая строка, стоящая на месте Fy., также строится путем реализации операций, отвечающих уравнению (3.40).

Перечисленные операции должны быть выполнены в каждом узле, где требуется провести преобразование системы координат.