1.2. Типы алементов 21

является представителем целого семейства конечных элементов. Используемый в совокупности с элементами того же типа, он описывает фермовые и пространственные рамные конструкции. В совокупности с элементами других типов, и особенно с пластинчатыми элементами, с его помощью обычно описывают подкрепленные элементы конструкции. Так как теоретические соотношения, связанные с указанным элементом, хорошо известны, в книге не отводится места для описания характеристик этого элемента. Более того, мы используем его в начальных главах книги для иллюстрации многих ключевых положений конечно-элементного анализа.

Основным элементом при конечно-элементном анализе является пластина, нагруженная в своей плоскости (условие плоского напряженного состояния). На рис. 1.1 (Ь) изображены треугольный и четырехсторонний плоско-напряженные элементы. К этому классу элементов можно отнести еще много элементов, имеющих различную форму в плане, однако они используются в весьма специальных случаях. Эти элементы называются основными не только благодаря их полезности при численном исследовании целого ряда прикладных задач проектирования, но также ввиду их приоритетной роли в истории развития метода конечных элементов. Теоретические работы на протяжении первых лет развития метода конечных элементов были целиком посвящены этому типу элементов.

Изображенный на рис. 1.1(c) сплошной (трехмерный) элемент представляет обобщение на трехмерный случай плоско-напряженного элемента. Тетраэдр и параллелепипед являются наиболее распространенными формами трехмерных элементов и играют важную роль при моделировании задач механики грунтов и скальных пород, а также конструкций, используемых в ядерной физике. Уместно напомнить, что фактически не существует других подходов при численном анализе поведения конструкции, с помощью которых решались бы реальные прикладные трехмерные задачи.

Одной из самых важных областей применения метода конечных элементов является расчет осесимметричных тел, изображенных на рис. 1.1(d). К этой области относится большое количество прикладных задач, включая расчет бетонных и стальных резервуаров, сосудов, содержащих ядерное горючее, роторов, поршней валов и двигателей ракет. Нагрузки, так же как и геометрические очертания, бывают обычно осесимметричными. Здесь изображен только треугольный элемент, хотя полезен также и четырехсторонний элемент, аналогичный изображенному на рис. 1.1(b).

Элементы типа изгибаемых тонких пластин используются не только для описания поведения плоских пластин, но также для представления оболочек и тонкостенных элементов. Конфигурация элементов схожа с геометрией плоско-напряженных элементов, причем наибольшее распространение имеют треугольные и четырехсторонние элементы рис. 1.1(e).

1.3. Некоторые приложения метода конечных элементов

Чтобы проиллюстрировать, каким образом используются описанные выше элементы в вычислительных задачах, возникающих при проектировании конструкций, а также объем и сложность указанных проблем, приведем ряд примеров численного анализа прикладных задач проектирования.

Развитие метода конечных элементов многим обязано работам исследователей, занятых проектированием аэрокосмической техники, поэтому не удивительно, что и.менно эта область исследований остается ведущей по количеству приложений метода конечных элементов. Рисунок 1.2 отрал<ает много аспектов использования метода конечных элементов при расчете конструкции самолета Боинг-747 [1.16]. Фюзеляж самолета состоит из тонких листов металла (обшивка), охватывающих несущую конструкцию, набранную из элементов, называемых шпангоутами и стрингерами. Силовые элементы крыла называются лонжеронами и нервюрами.

Опыт показал, что при расчете полей напряжений во всей конструкции можно не учитывать локальное выпучивание обшивки летательного аппарата. Поэтому обшивку можно представить состоящей из плоско-напряженных элементов, таких, как изображенные на рис. 1.1 (Ь) и (с) треугольные и четырехсторонние элементы, а несущую конструкцию можно смоделировать набором элементов типа изображенных на рис. 1.1(a). Расчет методом конечных элементов участка соединения крыла с фюзеляжем самолета Боинг-747 , изображенного на рис. 1.2(b), потребовал около 7000 неиз-

Осесимметричные оболочечные конструкции, изображенные на рис. 1.1(f), важны на практике так же, как и осесимметричные сплошные конструкции, однако здесь определяющие соотношения выводятся с использованием упрощающих предположений теории тонких оболочек. Теория осесимметричных тонких оболочек заполняет пробел между теорией изгиба и растяжения плоских пластин и теорией тонкостенных оболочечных элементов общего вида; эта теория позволяет выявить ключевые аспекты, возникающие при исследовании оболочек общего вида.

Если тонкостенная оболочечная конструкция искривлена, то для ее аналитического описания предпочтительно использовать криволинейные тонкостенные оболочечные элементы. К преимуществам указанных элементов относятся возможность более точного описания геометрии поверхности исследуемой оболочки и правильный учет взаимосвязи растягивающих и изгибающих усилий в оболочке. Типичные элементы, соответствующие закрученной в двух направлениях оболочке, представлены на рис. 1.1(g). Существует большое количество разнообразных элементов подобного типа.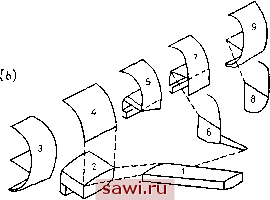

Рис. 1.2. Конечно-элементный анализ самолета Боинг-747 (из [1.16]) (а) Самолет Боинг-747 (заштрихованные области отвечают исследованным с помощью метода конечных элeмeнtoв участкам конструкции самолета). (Ь) Подконструкции, используемые в конечно-элементном анализе заштрихованных областей.

вестных переменных. Наличие столь большого количества неизвестных неудобно с точки зрения обработки начальных данных и выявления возникающих при счете ошибок. Поэтому на практике конструкцию обычно разбивают на части или, иными словами, иа подконструкции (суперэлементы) и каждая из подконструкции рассчитывается методом конечных элементов. На конечном этапе расчетов суперэлементы объединяются с помощью обычной конечно-элементной схемы. Вид разбиения на подконструкции при расчете