Литература

3.1. Beaufait F Rowan W, Н., Hoadley Р, G., Hackett R. M. Computer Methods oi Structural Analysis.-Englewood Cliffs, N. J.: Prentice-Hal, Inc., 1970.

3.2. Meek J. L. Matrix Structural Analysis.-New York. N. Y.: McGraw-Hill Book Co., 1971.

3.3. Wang C. K. Matrix A\etiiods ot Structural Analysis 2nd ed.-Scranton, Pa.: International Textbook Co., 1970.

3.4. Willems N., Lucas W. Matrix Analysis for Structural Engineers.-Englewood Cliffs, N. J.: Prentice-Hall, Inc., 1968.

3.5. RoseD. J., Willougiiby R. A. (eds.). SparseMatrice and Tiieir Applications.- New York, N. Y.: Plenum Press, 1972.

3.6. Fox R., Stanton E. levelopments in Structural Analysis by Direct Energy Minimization.-AIAA J., June 1968, 6, No. 6, p. 1036-1042. [Имеется перевод: Ракетная техн. и космон.- М.: Мир, 1968, №6.]

3.7. Nickel) R. Е., Wilson Е. L. Application of tiie Finite Element Metiiod to Heat Conduction Analysis.-Nuc. Eng. Design, 1966, 4, p. 276-286.

3.8. Gallagher R. H. Computational Methods in Nuclear Reactor Structural Design for High-Temperature Applications, Chяpteг 7. Thermal Analysis-Report ORNL-4756, July 1972.

3.9. Marcal P. V. Finite Element Analysis with Material Nonlmearities-Theoiy and Practice.-In: Finite Element Method In Civil Engineering, J. McCutche-on, M. S. Mirza, and A. Mufti, (eds).-Montreal, Quebec: McQill Univ., June 1972, p. 35-70.

Выражения для граничных условий в новых координатах можно включить в измененную глобальную матрицу жесткости [К]. В данном подходе при подсчете внутренних сил необходимо сначала преобразовать вычисленные перемещения к глобальной системе координат.

Альтернативным к вышеизложенному подходу служит подход, в котором элементы матриц жесткости и напряжений формируются непосредственно в терминах, соответствующих локальным системам координат. Это вносит определенные трудности при учете входных данных, так как условия закрепления задаются в узлах, а не на элементах; тем не менее процедура компактна и эффективна. Построение глобальной матрицы жесткости и другие операции осуществляются обычным путем. Однако требуются иные операции для включения всех указанных выше преобразований в узлах в единую глобальную матрицу преобразований. Этот подход алгоритмически прост, но оказывается эффективным лишь в том случае, когда в рассмотрение включено большое количество узлов всей конструкции.

Подходом, устраняющим алгебраические трудности, возникающие во всех представленных методиках, является процедура введения специального граничного элемента, как указано справа на рис. 3.15(a). Это специальный случай процедуры, определенной на рис. 3.15(d), где исключены степени свободы в направлении у .

3.10. Gallagher R. Н. Geometrically Nonlinear Finite Element Analysis.-In: Finite Element Mettiod in Civil Engineering, J. McCutcheon, M. S. Mirza, and A. Alurfi (eds.).-Montreal, Quebec: McGill Univ., June 1972, p. 3-34.

3.11. Kamel H., Liu D., ЛкСаЬе M., Ptiillipopoulos V. Some Developments in ttie Analysis of Complex Ship Structures.-In; Advances in Computational Methods in Structural Mechanics and Design, J. T. Oden, et al. (eds.).-Ala.: Univ. of Alabama Press, 1972, p. 703-726.

3.12. Walton W, C, Steeves E. C. A New Matrix Theorem and its Application for Establishing Independent Coordinates for Complex Dynamical Systems with Constraints.-NASA TR R-326, Oct. 1969.

Задачи

3.1. Постройте матрицу жесткости для четырехсегментной балки, изображенной на рис. Р3.1, используя прямой метод жесткости; £/=20 Юкдюйм.

Рис. P3.J.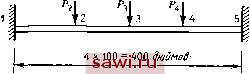

3.2. Постройте матрицу жесткости в задаче 3.1, используя методику конгруэнтных преобразований.

3.3. Сконденсируйте матрицу жесткости в задаче 3.1 к размерности 3X3, исключая угловые смещения.

3.4. Введите связь w=Wn в уравнениях жесткости задачи 3,3 и постройте редуцированную матрицу жесткости. Сравните решения для w при ограничениях и без них, положив Р4=4800 фунтов (остальные силы равны нулю).

3.5. Вычислите напряжения в элементах и узловые смещения для конструкции, изображенной на рис. Р3.5 (размеры даны в дюймах), используя прямой метод жесткости. Проведите вычисления в той последовательности, которая указана

Рис. Р3.5. (Линейные размеры даны в дюймах.)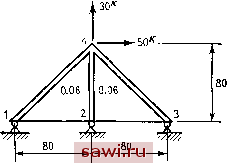

в разд. 3.2. Матрица жесткости для треугольного элемента, находящегося в плоском напряженном состоянии, приведена на рис. 5.4 ; £=10 фунт/дюйм; li=0.3; Л1 4=Л2-4=Лз 4=1.0 дюйм .

3.6. Исследуйте изображенную на рис. Р3.6 конструкцию, используя последовательность действий, оговоренных в задаче 3.5. (Разделите, как указано, прямоугольный элемент на два треугольных элемента.) £=10 фунт/дюйм, ц=0.3.

t= 0.006 а= 0.10

Рис. Р3.6. (Линейные размеры даны в дюймах, площадь А - в квадратных дюймах.)

1 = 0,12

1Б00 фунтоЗ

3.7. Вычислите смещение изображенной на рис. Р3.7 точки А в направлении х, используя прямой метод перемещений, £=10 фунт/дюйм, ц=0.3. Разделите, как указано, лист материала на четыре прямоугольных элемента. Матрица жесткости для прямоугольного пластинчатого элемента приведена на рис. 9.13. Учтите симметрию относительно оси к,

.> \а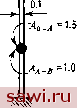

Рис. Р3.7. (Линейные размеры даны в дюймах, площадь А - в квадратных дюймах.)

3,8, Матрица жесткости для изображенной на рис. Р3.8 (линейные размеры даны в дюймах, площадь - в квадратных дюймах) конструкции задана в осях системы

Рис. Р3.8.