X - у. Постройте матрицу жесткости в терминах Р.,

(Симметрично)

10.0 -2.5 1.83

4.5 2.5

2.5 -2.5 -2.5 2.5

3.9. Исследуйте изображенную на рис. Р3.9 (размеры даны в дюймах) конструкцию согласно методике, оговоренной в задаче 3.5. Трапециевидную пластину разбейте на прямоугольные и треугольные пластины. Соответствующие матрицы жесткости приведены на рис. 5.4 и 9.13; £=20-10 фунт/дюйм, ц=0.2.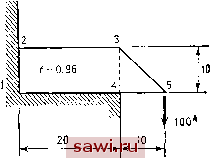

Рис. Р3.9. (Линейные размеры даны в дюймах.)

3.10. Постройте необъединенную глобальную матрицу жесткости f J и глобальную кинематическую матрицу [А] для конструкции из задачи 3.5. Вычислите на компьютере глобальную матрицу жесткости с помощью Ы]( к jlA].

3.11. Постройте необъединенную глобальную матрицу fk* J и глобальную кинематическую матрицу [А] для конструкции из задачи 3.6. Вычислите вручную или на компьютере глобальную матрицу жесткости с помощью преобразования [ДРГкЛД].

3.12. Постройте необъединенную глобальную матрицу жесткости Г к* J и кинематическую матрицу системы [А] для конструкции из задачи 3.7. Вычислите глобальную матрицу жесткости [к].

3.13. Обобщите утверждение (3.5), включив начальные смещения {Д } в вектор перемещений и соответствующие силы {Р } в вектор сил. Начальные смещения

Рис. Р3.14. Шиненные размеры даны в футах.)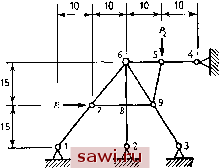

А= const

Е const

суть заданные величины, а соответствующие им силы неизвестны. Обобщите процедуру решения, определенную в (3.5), чтобы учесть указанные условия.

3.14. Исследуйте кинематическую устойчивость изображенной на рис. P3.I4 (размеры даны в фунтах) фермы с по.мощью процедуры исключения Гаусса - Жордана, примененной к трем уравнениям равновесия конструкции, т. е. исключите узлы 5-9.

3.15. Получите уравнения равновесия в матричной форме для изображенной на рис. Р3.15 (размеры даны в дюймах) фермы и примените процедуру исключения Гаусса - Жордана для выявления дополнительных сил (все площади равны).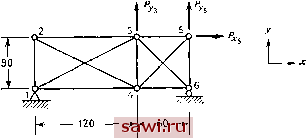

Рис. Р3.15. (Линейные размеры даны в дюймах.)

3.16. Рассматривая элементы 2-3 и 3-4 как подконструкций для конструкции из задачи 3.1, исключите Wg и как внутренние степени свободы и постройте матрицу жесткости конструкции относительно w, Q Щ t-

3.17. Изображенные на рис. Р3.17 элементы 1-2 и 2-3 имеют только крутильную жесткость k=GJlL. Вычислите углы закрутки 9 и 6, обусловленные при-

ложенными скручивающими моментами 1

М и М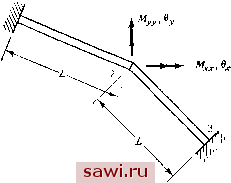

Рис. Р3.17.

3.18. Предполагается, что уравнения связи в задаче с п степенями свободы имеют вид lG]{A}={s), где [G] есть (лХп)-матрица. Разделите степени свободы на две группы и {Ас}(л г)х1- Постройте матрицу преобразований в внде (3.31)

(учитывая однако вектор {s}). Выпишите уравнения жесткости в редуцированной форме (т, е. уравнения жесткости в терминах {A})-

ОСНОВНЫЕ СООТНОШЕНИЯ ТЕОРИИ УПРУГОСТИ

в этой главе получим основные дифференциальные соотношения линейной теории упругости. Подробный вывод этих соотношений проводится в прямоугольной системе координат для двумерного случая. Этот случай в основном рассматривается в главах, в которых излагаются основы метода конечных элементов. Без вывода приведем также соотношения, которые обобщают результаты, полученные для двумерного случая, на трехмерные задачи. Обобщения на более частные случаи и системыкоординат отложи.ч до глав, в которых рассматриваются соответствующие типы конечных элементов.

Следует также заметить, что вывод указанных соотношений осуществляется простейшим способом с минимумом строгости. Данный подход соответствует уровню изложения, характерному для более ранних книг по теории упругости [4.1, 4.2] или сравнительно недавно вышедших курсов, которые можно назвать повышенными курсами сопротивления материалов [4.3, 4.4]. Более строгий уровень построения теории, включающий нелинейные аспекты и более общие типы поведения материала, читатель может найти в книгах [4.5-4.7].

В теории упругости имеются три системы соотношений: (1) дифференциальные уравнения равновесия; (2) соотношения, связывающие деформации с перемещениями, и условия совместности; (3) уравнения состояния материала. Для любого тела, имеющего конечные размеры, системы (1) и (2) дополняются граничными условиями. В данной главе выводится каждое из этих соотношений, а затем в общих чертах показано, как из совокупности указанных соотношений получить определяющую систе.му уравнений. В заключение приводятся некоторые замечания, касающиеся вопроса единственности решения задач упругости и его значимости для метода конечных элементов.