4.1. Дифференциальные уравнения равновесия

Для простоты изучим сначала равновесие бесконечно малого плоского элемента с действующими, как указано на рис. 4.1, нормальными а, Оу и касательной tj, компонентами напряжения, а также компонентами объемной силы (т. е. силы на единицу объема) X uY. Объемные силы могут возникнуть по разным причинам, однако в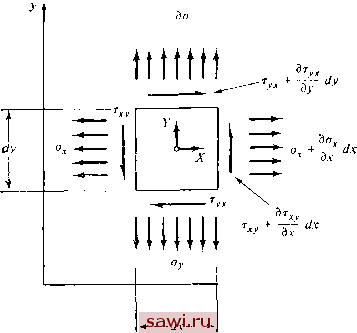

Рис. 4.1.

настоящем рассмотрении они введены главным образом для того, чтобы учесть действие сил инерции в динамическом случае. Предполагается, что компоненты напряжения, как показано на рис. 4.1, постоянны в направлении, перпендикулярном их действию; иными словами, хотя и меняется вдоль оси х, она считается постоянной на грани шириной dy. Проводя более тонкий анализ, учитывающий изменение компоненты напряжения вдоль грани, можно показать, что получаются члены более высокого порядка по сравнению с членами, рассматриваемыми в классической линейной теории упругости. Записывая условие равновесия в проекции на ось х (толщина грани в направлении, нормальном плоскости х-у, равна

единице), имеем

2/=. = 0= [<y,+ -dx)dy-a,dy + Kdxdy +

dy) dx-Xy,

и после приведения подобных членов получим

. - + х = 0.

dx (4.1) (4.2а)

дх ду

Аналогичные рассуждения для направления вдоль оси у дают

ду дх *

(4.2Ь)

Естественно, что в плоском случае должны удовлетворяться три условия равновесия, причем третьим из них является равенство моментов относительно оси, нормальной к плоскости. Наложение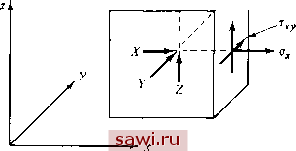

Рис. 4.2.

ЭТОГО условия приводит к тому, что Тху=!/х- Таким образом, уравнения (4.2а) и (4.2Ь) представляют собой искомые уравнения равновесия плоской задачи теории упругости. Не составляет труда обобщить эти выражения на трехмерный случай (с объемными силами X, Y и Z). (См. рис. 4.2, где изображены компоненты напряжения и силы.)

-fX = 0,

(4.3)

Конечно-элементная формулировка задачи в определенных случаях опирается на выбор поля напряжений. Поэтому необходимо либо выбирать поля таким образом, чтобы они удовлетворяли дифференциальным уравнениям равновесия, либо проверять, удовлетворяют ли этим условиям выбранные функции, которые априори задавались без учета указанных условий. Например, если выбрать плоское поле напряжений, компоненты которого тождественно равны константам 0=01, ау=а.2, тг,=аз, то очевидно, что условия (4.2а) и (4.2Ь) выполняются. Более сложное поле, имеющее вид

где fli, . . ., 5-константы, также удовлетворяет уравнениям (4.2а) и (4.2Ь). С другой стороны, поле

Ox=ai-\-a2X, Oy=a3+aiy, т:ху=а

не удовлетворяет дифференциальным уравнениям равновесия до тех пор, пока не обратятся в нуль коэффициенты и 4 (a2= j=0).

Удобно находить поля напряжений, удовлетворяющие дифференциальным уравнениям равновесия, с помощью введения функций напряжения. Функции напряжения представляют собой функции, которые будучи продифференцированы согласно соответствующим правилам, дают компоненты напряжения, автоматически удовлетворяющие дифференциальным уравнениям равновесия. Плоское напряженное состояние можно охарактеризовать одной такой функцией Ф, называемой функцией напряжения Эри и определяемой соотношениями

Очевидно, что в отсутствие объемных сил (Х = У=0) указанные поля напряжений автоматически удовлетворяют уравнениям (4.2) при любом выборе Ф. Рассмотрим, например, Ф=а-\-ах-\-ау-\-iUiX+lау -азху. Тогда Ox=ai, Оуа, ху=С1з, что совпадает с вьпиеприведенным примером.

Фун1Щии напряжения можно построить также для трехмерной теории упругости, теории изгиба пластин и других отдельных случаев упругого деформирования. Так, при расчете изгиба пластин методо.м конечных элементов, особенно полезно знание функций, называемых функциями напряжения Саусвелла. Эти функции рассматриваются в гл. 12. Основные трудности, связанные с введением функций напряжения, заключаются в том, что последние не имеют четко выраженного физического смысла. Это усложняет задание граничных условий и исследование других ключевых аспектов в процессе решения любой практической задачи.