4.2. Граничные условия для напряжений

4.2. Граничные условия для напряжений

Дифференциальные уравнения равновесия должны выполняться в любой внутренней точке тела. Помимо этого, необходимо учесть условия равновесия на границе тела (статические граничные условия). Рассмотрим, согласно рис. 4.3, границу двумерной области, на которой действуют заданные поверхностные усилия и Ту*

Л, ds-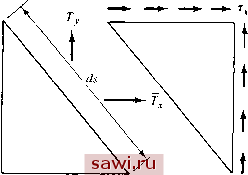

Рис. 4.3.

Обычно эти поверхностные силы определяются как силы, направленные вдоль оси X к у н действующие на единицу площади поверхности, расположенной под некоторым углом к указанным осям. На рис. 4.3 изображен участок поверхности длиной ds для плоского напряженного состояния (так как рассматривается пластинка единичной толщины, то площадь поверхности численно равна длине ds). Символами 1 и 1у обозначены соответственно косинусы углов между нормалью к поверхности и осями х и у. Из условий равновесия в направлении оси х имеем

Txds==a,(l,db) + x[l ds)

а для направления вдоль оси у -

FylyOy--lxXxy

(4.5а)

(4.5Ь)

* В этой книге все задаваемые величины (граничные усилия, перемещения) обозначаются символами с чертой сверху.

В методе конечных элементов рассматриваются условия равновесия не только во внутренних точках конструкции или на ее внешних поверхностях, но и в точках соприкосновения элементов. На границе каждого из соприкасающихся элементов в середине имеется некоторое напряженное состояние, поэтому уравнения должны выполняться в каждой точке соприкасающихся граней. На рис. 4.4(a)

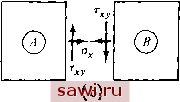Рис. 4.4.

изображены два соседних элемента А н В, поверхность соприкосновения которых проходит по оси у глобальной системы координат. На поверхности раздела не действуют внешние нагрузки. Для выяснения условий равновесия на границе элементов разделим элементы, как показано на рис. 4.4(b). В соответствии с ориентацией поверхности раздела имеем /j,=0, lx=l, и уравнения (4.5) сводятся к уравнениям Тх=Ох, Ту=Хху. ,

Следовательно, если граница раздела между элементами проходит вдоль оси у, то для выполнения условий равновесия требуется лишь, чтобы нормальная компонента напряжения и касательная компонента ту на этой границе были непрерывны. Разрешается, чтобы нормальная компонента напряжения Оу, если она существует, была разрывной при переходе этой границы в направлении X. Если поверхность раздела наклонена под некоторым углом к осям X и у, то нормальные и тангенциальные компоненты усилий на ненагруженной поверхности (Тп и Ts) должны быть непрерывны на границе, разделяющей элементы. С каждой стороны от поверхности раздела два усилия выражаются через три компоненты напряжения. Поэтому, несмотря на то что компоненты напряжения в направлении координат могут изменяться при переходе от одного элемента к другому, условия равновесия при переходе через поверхность соприкосновения элементов все же сохраняются.

Перед нами снова возникла необходимость ввести символ, кото-)ый обозначал бы совокупность компонент некоторой переменной. Лричем этот символ должен отличаться от символа, соответствующего вектору, который задает значения этих компонент в той или иной точке. Вводимый таким образом символ есть тензор напряжений а, который включает в себя компоненты . . . t; этот символ будем записывать жирным шрифтом без скобок. Если нужно перечи-

СЛИТЬ компоненты тензора а, то будем записывать их в виде вектор-строки или вектор-столбца в следующем порядке: \ OxOy ахуХу T.xJ. Аналогично поле заданных поверхностных усилий будем обозначать через Т и считать, что этот символ относится к совокупности Тх Ту J , а объемные силы объединим символом Х= \ XYZJ. Символом же, соответствующим вектору, обозначаются привычные понятия матрицы-строки [ J или матрицы-столбца { }. Если, например, напряжения для плоского напряженного состояния определить в двух точках, скажем 1 и 2, то запись примет вид

{ofL (Ух, (г/, -Сху, Ох, Оу XxyJ.

4.3. Соотношения, связывающие деформации с перемещениями, и условия совместности

При формулировке метода конечных элементов на основе метода перемещений очень важны кинематические дифференциальные соотношения, связывающие деформации с перемещениями. Наоборот, дифференциальные уравнения равновесия (условия статики), приведенные в разд. 4.1, не играют столь существенной роли при этом подходе.

Рис. 4.5.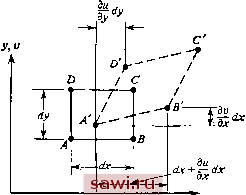

Для вывода соотношений между деформациями и перемещениями рассмотрим малое смещение из недеформированного состояния ABCD в деформированное состояние ABCD для бесконечно малого элемента, изображенного на рис. 4.5. В результате деформации имеем для малых (линейных) деформаций

(ABr=(dx + pxy + (lidx]

(4.6а)