наличии в нем напряжений. У изотропного материала зависимость деформаций от напряжений неизменна при ортогональном преобразовании координат. На рис. 4.7(a) изображено, как прикладываемое к образцу напряжение в направлении оси х вызывает деформацию образца в обоих направлениях х а у. Вдоль

Рис. 4.7.

И Л (ь)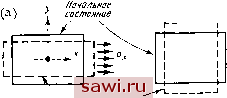

Дерормиройанное-состояние

оси x деформация равна попросту qJE. Образец сжимается и в направлении оси у, так как коэффициент Пуассона л отличен от нуля, поэтому в этом направлении деформация равна -csJE. Аналогично наличие напряжения вызывает деформации в направлении осей х и у, равные соответственно -[хо/ и OylE (как показано на рис. 4.7(b)). На значения относительных удлинений вдоль осей х и у не влияет наличие деформации сдвига, изображенной на рис. 4.7(c), которая связана со сдвиговым напряжением соотношением

2(l+i)

Ух - £ ху

В результате суперпозиции и записи соотношений в матричной

форме (с 0= L <а; ху J . 8= 6. Еу Ту J ) ПОЛуЧИМ

е=[Е]-Ч

[Е]- = -

1 -и О

(1-Ц)/2.

О 2(1+1х)

(4. И)

(4.12)

(4.13)

Матрица [Е] называется матрицей жесткости материала, а [E]~- матрицей податливости материала. Аналогично выражению (4.10) можно непосредственно обобщить вышеприведенные соотношения на случай наличия начальных деформаций е =

J , что приводит к соотношению е=[Е]-1о+е .

(4.14)

Начальные деформации представляют наибольший интерес в задачах термоупругости, где е!( =е =аГ, у]Ру=0, для изотропного тела с коэффициентом линейного расширения а и отклонением температуры от температуры ненапряженного состояния на Г.

Наиболее часто применяемый подход при построении конечно-элементной модели - подход, при котором задаются функции перемещений,- требует, чтобы напряжения были выражены через деформации. Поэтому, обращая уравнение (4.14), получим

а=[Е]е-[Е1е . (4.15)

Теперь благодаря матричным уравнениям (4.14) и (4.15) в нашем распоряжении имеется достаточно общее представление механических свойств материала. Проводя обобщения на шестимерные векторы а и е, можно охватить все разнообразие задач трехмерной теории упругости. Полностью заполненная матрица [Е] размерностью 6x6 определяет общий случай анизотропного материала, который обладает различными свойствами в различных направлениях. Много частных случаев поведения материала находится в диапазоне между изотропией и полной анизотропией. Так, в частности, сюда можно отнести ортотропные материалы, имеющие три взаимно перпендикулярные плоскости упругой симметрии. В последующих главах будет подробно представлен ряд матриц [Е] и [Е]~1 специального вида, отвечающих требованиям соответствующей конечно-элементной модели. Важным свойством всех матриц жесткости и податливости для рассматриваемых здесь материалов является их симметричность (см. соотношения (4.12) и (4.13)).

Пока достаточно отметить, что метод конечных элементов особенно хорош при решении задач со сложными жесткостными свойствами материала. Из дальнейшего будет видно, что матрица [Е] (или обратная к ней матрица) легко обрабатывается в алгоритмах численного интегрирования. Ограничения, накладываемые на сложность и представления жесткостных характеристик материала, часто диктуются практикой: для большинства практических заач трудно располагать большей информацией о механических характеристиках материала, чем полученной в результате эксперимента информацией о зависимости напряжений от деформаций для орто-тропного материала в двумерном случае. Исключение составляют слоистые пластины с ортотропными слоями (механические характеристики слоев можно определить экспери.ментально, а затем вычислить характеристики всей слоистой пластины) и композитные материалы (например, стекло-волокнистые композиты). Благодаря особой роли композитов как ортотропных материалов, применяемых на практике, публикации, касающиеся их разработки и использования, представляют отличный источник информации для детального построения вполне общих соотношений, задающих жест-костное поведение материала (см. [4.8]).

4.5. Дифференциальные уравнения равновесия и совместности 1J9

4.5. Дифференциальные уравнения равновесия и совместности

Приведенные выше системы уравнений можно объединить с целью получения альтернативных форм дифференциальных уравнений, точное решение которых будет удовлетворять и исходным уравнениям. Эти альтернативные формы называются соответственно дифференциальными уравнениями равновесия и совместности.

Сделаем несколько замечаний относительно мотивировки построения указанных дифференциальных уравнений. Ранее были независимо сформулированы два набора условий: статические и динамические. Статические условия записываются исключительно через статические переменные (напряжения или функции напряжений). Кинематические условия записываются только через кинематические переменные (перемещения или деформации). Для единственности решения необходимо связать статические и кинематические переменные. Это осуществляется с помощью введения определяющих соотношений.

Выведем сначала дифференциальные уравнения равновесия, так как подход, использующий при построении конечно-элементной модели метод жесткостей (или метод перемещений), одновременно может служить подходом, позволяющим получить приближенное решение этих уравнений. Для простоты исключим из рассмотрения объемные силы и начальные деформации (Х = 7=0, {8 }=0). Вывод искомых уравнений заключается в построении соотношений, связывающих напряжения с перемещениями, с последующей подстановкой этих соотношений в дифференциальные уравнения равновесия. Например, подставляя соотношения, связывающие дефор-.мации с перемещениями, в уравнение состояния для а, получим

. = Г=]12а+те]125- (4.16)

Аналогичные операции нужно провести также для Оу и iy. Далее, подставляя полученные соотношения в дифференциальные уравнения равновесия (уравнения (4.2а) и (4.2Ь)), имеем

ди , L-цац

дх 2 ду 2 дх ду

4{\-у.)дхдц-

Е аи (4-17)

2 (1 -ц) дхду

Если можно найти отвечающие кинематическим граничным условиям непрерывные однозначные поля перемещений, которые удовлетворяют вышеприведенным соотношениям и соответствующим граничным условиям, то будет найдено искомое точное решение. Это и есть теорема единственности.