Задачи

4.2. Ниже в полярных координатах приводятся уравнения равновесия и соотношения, связывающие деформации и перемещения при плоском напряженном состоянии. Уравнения состояния идентичны соотношениям, записанным в прямо-

Рис. Р4.2.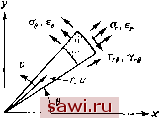

угольной системе координат. Выпишите определяющие дифференциальные уравнения равновесия с учетом тепловой деформации.

ди дг

и , I dv

дОг . 1 дтгв

Ог - Ов

= 0,

1 ди .dv V

УгО-у 3Q+Tr~T

4.3. Сформулируйте линейные дифференциальные уравнения равновесия для трехмерной задачи теории упругости, учитывая сначала зависимость напряжения от трех координат, а затем исключив члены более высокого порядка малости.

4.4. Используйте приведенную ниже функцию перемещений для построения матрицы жесткости, соответствующей изображенному на рис. Р4.4 элементу в форме

Рис. Р4.4.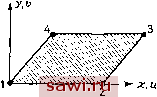

параллелограмма. Проверьте, удовлетворяет ли эта функция: (а) условиям равновесия внутри элемента, (Ь) условиям равновесия на границе элемента, (с) условиям непрерывности между элементами.

и = а1Х-\-а2у+аз(ху- y+Ot, u = af,x-\-aey + a, (ху--у+а.

4.5. Постройте матрицу связи напряжений с дефориациями [Е] для плоской деформации ортотропного материала. В итоге она должна связывать а= L ху J l.xyyxy J Вэтом случае Тд.2=т2=Ог=0. Упругие модули суть £.,£j Gy. коэффициент Пуассона, отвечающий деформации, направленной вдоль оси у, вызванной напряжением в направлении оси х, равен и т. д.

4.6. Проверьте, выполняются ли для элемента, изображенного на рис. P4.J, и для приводимого ниже поля перемещений уравнения равновесия. Что значит

с физической точки зрения, что эта функция не удовлетворяет условиям равновесия?

и = AiUi + iVjUj + n3u3 + niui,

/V, = (1 -хЫ (1 - t!y), /V2 = (xlx) (1 -у1уз),

N3(X/X2) (У/Уз), Л4=(1-(у/Уз).

4.7. Смещения на границе элемента, изображенного ниже, описываются с помощью функций

(2s-a)(s-a) 4s (g-s) s (2s-a)

Определите нормальные и тангенциальные усилия Т и 7 соответствующие этим перемещениям.

Рис. Р4.7.

4.8. Пусть Of, Фа и Фд - трехмерные функции напряжений, определяемые следующим образом:

-дудх- ° -дгдх дхду

дудх

1 д /дФг дФ дФз\

2 дг \ дх ду

\ д ( дФ-, . аФа дФз\

*~ 2 дх\ дх ду дг )

} д (дФг ЭФа дФз\

2 ду \ дх д,/ дг )

Докажите, что они удовлетворяют дифференциальным уравнениям равновесия и выведите соответствующие им уравнения совместности.

ПРЯМЫЕ МЕТОДЫ ПОСТРОЕНИЯ ЭЛЕМЕНТОВ

Начиная сданной главы, приступим к выводу соотношений между силами и перемещениями для элементов. При этом рассмотрим два подхода: прямой метод и метод взвешенных невязок.

В прямом методе построение соотношений для элемента осуществляется непосредственно с помощью учета приведенных в предыдущей главе трех систем уравнений теории упругости; уравнений равновесия, соотношений между перемещениями и деформациями, а также уравнений состояния. Этот метод особенно полезен при выяснении фундаментальных соотношений между конечно-элементной аппроксимшщей и реальной конструкцией. Так, этим методом будет проведено теоретическое обоснование построений, проведенных в разд. 2.2 и 2.3. Прямому методу присущи черты, свойственные и другим подходам к построению конечно-элементной модели. Особенно это затрагивает вопросы задания сил, если известны напряжения, и деформаций, если известны перемещения. Этот подход включает основные положения, использованные на ранней стадии развития метода конечных элементов [см. 5.1, 5.2]. Однако область применения прямого метода ограничена: его трудно или даже невозможно применять при выводе соотношений для усложненных элементов и в некоторых специальных задачах.

В свою очередь область применения метода взвешенных невязок [5.3] практически неограниченна, и, как оказалось, он обладает достоинствами, отсутствующими у альтернативных подходов. Один из вариантов этого подхода приводит к формулировке, идентичной той, к которой приходим при применении описанных в гл. 6 вариационных принципов. Для некоторых классов нелинейных задач методом взвешенных невязок можно вывести соотношения, которые нельзя получить с помощью классических вариационных принципов [см. 5.4, 5.5]. Кроме того, этот подход помогает уяснить физические основы таких вариационных принципов, как экстремальные принципы для потенциальной и дополнительной энергий.