(5.14а)

где itJ = lN,N,N,N, \,

/V, = (l+2£ -3E), /V, = (3r-2E=),

причем l=x/L.

Деформации в случае изгиба равны кривизнам (вторым производным), т. е. w . Следовательно,

cc.=LNJ {Л}, (5.15)

(5.15а)

Кроме того, напряжения в этом случае суть внутренние изгибающие моменты Ш, и определяющее соотношение запишется в виде

m = EIw . (5.16)

Так как вторые производные в (5.15а) изменяются линейно внутри элемента, то кривизна может быть определена однозначно, если заданы w в узлах 1 и 2. Согласно (5.15), получим

-6 4L 6 2L 6 ~2L -6 -4L

>=[D]{A}. (5.15b)

= [A]{a}.

(5.8b)

Рассматривая условия равновесия сил, необходимо заметить, что внутренние моменты ОТ, и в узлах 1 и 2 соответственно считаются положительными, если им отвечает положительная кривизна (см. рис. 5.1). Поэтому a3?i=Mi, а 3)?2=-Mj. Можно применить условия равновесия для моментов, чтобы выразить и р2 через ilJli, и Ш, и, объединив всю систему уравнений, записать

-1 1

L О т

[м, L о -L.

Кроме того, так как требуется на двух концах элемента связать моменты с кривизнами, необходимо записать уравнение изгиба (5.16) в расширенном виде *

{a l[=[E]{w }, (5.16а)

*) Строго говоря, л и £ относятся соответственно к полю напряжений а и полю деформаций е. В данном случае рассматриваются векторы узловых напряжений ({a]=[ W.lMlj) и узловых деформаций ((е}= Lmiimia J ). Чтобы не вводить новых обозначений, в обоих случаях используются одинаковые символы.

Т О О I

гН[Е]{е}.

Окончательно, объединяя (5.15Ь), (5.16а) и (5.8Ь) в виде произведения [к]=[А] [Е] [D], получим

6

-3L 2L (Симметрично)

-6 +3L 6

-3L 3L 2L

(5.17)

Вновь матрица жесткости была получена без учета в явном виде условий равновесия внутри элемента, которые для указанного элемента при отсутствии разрывов задаются уравнением

d*w/dx=0. (5.18)

Очевидно, что четвертая производная кубического полинома, задаваемого формулой (5.13), равна нулю, поэтому приведенное выше условие выполняется. Условие равновесия определяется простым суммированием сил и моментов в узлах, как указано в гл. 3.

Интуитивно можно предполагать, что в узлах должны выполняться условия непрерывности угловых смещений для изгибаемых элементов. Следовательно, условия непрерывности смещений в узлах глобального конечно-элементного представления требуют непрерывности как w, так и 6. Рассматриваемое представление удовлетворяет этим условиям. Так как оно удовлетворяет всем условиям равновесия, если нагрузки приложены только в узлах, то получаемое в этих случаях решение является точным. Мой?но построить приближенное поле перемещений (например, линейное поле, выраженное только через Wi и w, как в конечно-разностных методах) и, если в глобальном представлении используется конечное число сегментов, получить приближенное решение задачи.

Представление поля перемещений с помощью функции формы (5.5), (5.14) играет центральную роль в обоих иллюстративных примерах. Хотя понятие функции формы обсуждается более подробно в последующих главах, в особенности в гл. 8, важно отметить ее основные свойства, приступая к изучению способов построения элементов. Рассмотрим сначала случай, когда поле (или пробная функция) независимой переменной А выражается только в терминах значений Д; указанной переменной в заданных точках. Стержневой элемент (5.5) является примером указанного случая. При этом функция формы Ni определяется таким образом, что принимает значение, равное 1 в узле, где задана величина Д;, и равное нулю в других узлах, отвечающих остальньш степеням свободы. Это сделано для то-

ГО, чтобы A = Aj В узле, соответствующем А. Причина, побудившая назвать Nt функцией формы, теперь ясна: она характеризует изменение переменной А в области, занимаемой элементом, для А; = 1 и при фиксированных остальных степенях свободы. Сказанное иллюстрируется на примере стержневого элемента на рис. 5.2.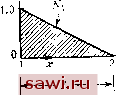

1.0--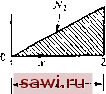

Рис. 5.2.

В некоторых случаях описание независимой переменной включает степени свободы в виде производных в заданных точках. Например, представление ш для изгибаемого элемента (5.14) с помощью функции фор.мы содержит в качестве степеней свободы производные от цу(в1 и бг) в концевых точках. Функции формы, умножаемые на эти степени свободы, должны иметь размерности, которые обеспечат появление членов, имеющих размерность перемещения. Поэтому в случае балочного элемента множители при 9i и бз в (5.14) имеют размерность длины (перемещения), так как 9i и бг измеряются в радианах.

5.2. Треугольный плоско-напряженный элемент

Проиллюстрируем прямой метод построения уравнений жесткости элемента на примере треугольного плоско-напряженного элемента, изображенного на рис. 5.3 и 5.4. Элемент имеет постоянную толщину t, его материал изотропен, и для удобства рассмотрения элемент расположен так, чтобы одна из его сторон лежала на оси х. Этот иллюстративный пример заслуживает особого внимания, так как, во-первых, рассматривается более общее напряженное состояние (двумерное) и, во-вторых, получающиеся уравнения жесткости приводят к приближенным решениям дифференциальных уравнений, определяющих задачи глобального анализа, и, в-третьих, изучаемый элемент имеет первостепенное значение во всех областях практических приложений.

Поведение элемента, как видно из рис. 5.4, описывается шестью степенями свободы:

{А}= Hi, из Vi Уа Vaj,

(5.19)