ПШГСЕШ

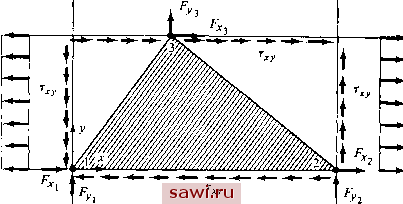Рис. 5.3. Способ представления граничных напряжений в треугольном элементе для подсчета узловых сил.

н так как направления х к у равноправны, то выбирается по три параметра для описания как и, так и v.

и=а1+агх+азу, va+ax+ugy. (5.20)

Заметим, что эти выражения являются полными линейными полиномами. Вычисляя и в узлах 1, 2 и 3, получим

= [В ]{а},

(5.21а)

откуда после обращения матрицы и подстановки в (5.20) имеем и=Л/,и,+Л/, ,+Л/зи (5.21а)

(хУз-хУз-хУ + ХзУЬ г=(ху,-х,у), N, = j-.

[к] =

У1 =

yi =

1+ А

Xi-1 - X) - Хх

Уз-2 = Уз - Уг

Рнс. 5.4. Матрица жесткости изотропного плоско-напряженного треугольного элемента с постоянной деформацией внутри элемента.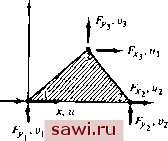

о

Те же функции формы получаются и для г, поэтому функция, задающая смещение v, имеет вид

v=NiVi+N,v,+N3V3. (5.21b)

Если теперь учесть соотношения между перемещениями и деформациями в плоской задаче теории упругости (4.7а, Ь, с) и применить их к (5.21а, Ь), то получим соотношение (5.6с), в котором

Ль. Лг.х Лз.. О О О О О О Лх.. Л., Лз.,

[D] =

Лз. J

(5.22)

где yVj, я означает производную по л; и т. д.

Для плоского напряженного состояния матрица [Е] задается выражением (4.12), поэтому, чтобы завершить построение основных матриц элемента, необходимо лишь задать матрицу связи между напряжениями и узловыми силами [А]. Это можно выполнить в результате непосредственного преобразования граничных напряжений в узловые силы. Для силы F например (см. рис. 5.3), имеем

Fx, = 4 [Ув<У.~х,Тху + (х-х,) tj.

Применяя эту процедуру для определения каждой узловой силы, получим соотношение (5.8а), в котором

{P\==LFx,fx,Fx- F...F..

[А] =4

Матрица жесткости для рассматриваемого элемента вычисляется согласно (5.10) в результате перемножения матриц [А] [Е] [Dl и использования выписанных выше соотношений. Эта матрица представлена на рис. 5.4.

Как и для предыдущих примеров, изучим те аспекты упругой задачи, которые явно не затрагивались выше. Деформации е постоянны внутри элемента, так как они получены в результате дифференцирования линейного поля перемещений. Напряжения, выражаемые через деформации с учетом упругих констант, также постоянны. Поэтому дифференцированные уравнения равновесия (4.3), включающие операции дифференцирования напряжений, вьшолня-