5.4. Прямой метод при решении физических задач 141

Преобразование узловых перемещений в поле деформаций

e=[D]{A}. (5.6с)

Преобразование узловых смещений в поле напряжений

o=[S] {Л}. (5.7а)

Преобразование узловых смещений в узловые напряжения

{а}=[5] {А}. (3.9)

Преобразование узловых напряжений в силы

{F}=[A1{0}. (5.8а)

5.4. Прямой метод при решении физических задач

С помощью прямого метода можно строить конечно-элементную модель физических процессов не менее успешно, чем при расчете упругого деформирования. Рассмотрим, например, одномерную задачу стационарной теплопроводности. Изучение этого процесса представляет практический интерес для проектировщиков, имеющих дело с задачами расчета термических напряжений, в которых весьма желательно иметь возможность единообразного подхода при расчете полей температуры и напряжений.

Рис. 5.6.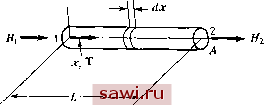

Рассматривается изображенный на рис. 5.6 изолированный стержень. Выделим одномерный элемент с площадью поперечного сечения А, длиной L и имеющий коэффициент теплопроводности и. Найдем соотношения между температурами (Гь Га) (°F) в точках 1 и 2 и значением теплового потока в этих точках (Ни Я а) (БТЕ).

В качестве определяющего соотношения выберем в данном случае закон теплопроводности Фурье

h-cTCIdx, (5.23)

где h - стационарный тепловой поток на единицу площади (БТЕ/ /фут ). Знак минус означает, что тепловой поток направлен в сторону уменьшения температуры. Согласно предьщущим построениям

ДЛЯ одномерного стержневого элемента, представим Г в виде

откуда

L j L

(5.24)

Полный тепловой поток в точке 1 равен Hi=hA, а в точке 2 Hi=hA (знак минус возникает из-за того, что положительное направление для Hi соответствует в этом узле тепловому потоку во внешнюю среду). Объединяя эти соотношения с соотношениями (5.23) и (5.24), находим, что

1 -1 -1 1

(5.25)

Набор коэффициентов в правой части уравнения называется матрицей теплопроводности элемента.

Кроме того, с помощью прямого метода можно построить матрицы теплопроводности для плоских треугольных элементов и других простых элементов. Аналогично можно построить соответствующие матрицы для конечных элементов в задачах фильтрации, электромагнетизма, расчета потенциального течения жидкости. Однако, как было замечено, чтобы использовать более сложные элементы и рассматривать более сложные физические аспекты перечисленных процессов, необходимо привлекать более тонкие теоретические концепции. Одна из таких концепций применяется в следующем разделе.

5.5. Метод взвешенных невязок

При использовании метода конечных элементов для решения задач, не связанных с механикой твердого деформируемого тела, требуется более общий подход к построению соотношений для элемента. Таким подходом является метод взвешенных невязок (МВН) [5.3]-В методе взвешенных невязок считается, что выбранная для аппроксимации независимой переменной в задаче математической физики пробная функция (т. е. рассматриваемые в разд. 5.1 и 5.2 полиномы), вообще говоря, не удовлетворяет соответствующим определяющим уравнениям. Так, подстановка пробной функции в определяющие дифференциальные уравнения приведет к невязке, обозначенной через R. Чтобы получить наилучшее решение, требуется минимизировать интеграл от невязок по области, рассматриваемой в задаче, т. е.

j R-d(yol):=mm.

Можно расширить возможности метода, вводя в подынтегральное выражение минимизируемого функционала взвешенные величины невязки. Введение весовых функций позволяет обратить в нуль интеграл от взвешенных невязок. Обозначая весовую функцию через ф, приходим к более общему соотношению

5 /?Ф(уо1) = 0. (5.26)

Таким образом, (5.26) представляет собой общее утверждение в методе взвешенных невязок.

Весовые функции можно выбирать различным образом и каждый конкретный выбор отвечает соответствующему критерию в МВН. Обратимся к методу Галеркина, так как этот метод приводит к таким же уравнениям, как и при использовании обычных энергетических или вариационных подходов [5.6-5.8].

Чтобы описать МВН, использующий критерий Галеркина, рассмотрим определяющее дифференциальное уравнение

S)(A) = 0, (5.27)

где S> - дифференциальный оператор, а Л - независимая переменная, которую нужно аппроксимировать с помощью А в виде (5.5), т. е. с помощью суммирования п функций формы Nt, помноженных на соответствующие степени свободы А(. Подставляя А в (5.27), получим невязку

R = S>(K)=Q. (5.28)

Согласно критерию Галеркина, функции формы Nf определяются как весовые функции. Поэтому для каждого i имеем

5 A/.(A)d(vol) = 0 (1=1.....п), (5.29)

что приводит к общему числу уравнений, равному п.

Уравнения (5.29) относятся к узлам внутри области и не учитывают граничных условий, например заданных внешних нагрузок или Перемещений. Чтобы учесть граничные условия, требуется проинтегрировать по частям интегралы (5.29), то приводит к появлению интегралов по области и границе.

Проиллюстрируем предлагаемый метод, применяя его сначала для построения уравнений жесткости стержневого элемента, обсуждавшегося ранее в этой главе, с добавлением распределенной нагрузки q согласно рис. 5.7. Требуется построить соотношения в терминах перемещений, где А=ы. Для этого случая определяющее дифференциальное уравнение получается подстановкой соотношений между напряжениями и перемещениями [ох=Е (duldx)] в