рис.

5.3. Постройте матрицу жесткости [S] для прямоугольного элемента в плоском напряженном состоянии, который сформирован на базе функций формы, приведенных в задаче 5.2. Выбрать в качестве переменных величины х у.

5.4. Постройте матрицу жесткости для приведенного в разд. 5.3 треугольного плоско-напряженного элемента из ортотропного материала.

5.5. Сформулируйте процедуру построения матрицы жесткости балочного элемента на основе метода взвешенных невязок с критерием Галеркина и проиллюстрируйте ее на примере построения первой строки матрицы (f j в зависимости от %, 9i, w, Эа).

5.6. Выведите, используя метод взвешенных невязок с критерием Галеркина, необходимые интегральные соотношения для непосредственного построения матриц жесткости элементов в плоском напряженном состоянии, если известны поля перемещений.

5.7. Обобщите прямой метод на непосредственное построение матриц податливости элементов и проиллюстрируйте подход построением матрицы податливости балочного элемента.

5.8. Обобщите прямой метод на непосредственное построение матриц связи сил с перемещениями смешанного вида (см. гл. 2) и проиллюстрируйте это на примере балочного элемента.

5.9. Постройте матрицу теплопроводности для плоского треугольного элемента, используя прямой метод в предположении линейного характера распределения температур: Г=Л1Г1+Л2Г2-1-ЛзГз, где Tj, и Г3 -значения температуры в узлах элемента.

5.10. Дифференциальное уравнение, описывающее выпучивание балки, имеет вид

= 0.

Используя метод взвешенных невязок с критерием Галеркина, получите интегральную форму соотношений, необходимую для построения соответствующих уравнений жесткости элемента. Предположите, что поле перемещений аппроксимируется в виде w=N,Wi-i-NiQi+Ni-l-NiQi, где Ni, , , . , задаются с помощью (5.14а).

Л/2. 2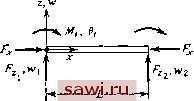

Рис. Р5.10.

ВАРИАЦИОННЫЕ МЕТОДЫ ПОСТРОЕНИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ

Вариационные или энергетические методы исследования конструкций образуют мощный и широко применяемый подход к построению соотношений для конечных элементов. Простейшие варианты этих методов используются для расчета инженерных конструкций уже более ста лет. Однако некоторые усложненные варианты вариационных и энергетических методов так же современны, как и сам конечно-элементный анализ элементов, и их развитие, по-видимому, обусловливалось желанием создать новую теоретическую основу метода конечных элементов. Так или иначе, последние работы в этой области дают всесторонний анализ возможных вариационных принципов строительной механики, в частности определяют область их применения и выявляют присущие им недостатки.

В данной главе соответствующие вариационные принципы механики конструкций описываются с учетом их дальнейшего использования для построения конечно-элементных соотношений. Применение этихл принципов при построении соотношений для всей конструкции излагается в гл. 7. Таким образом, предполагается, что соотношения между силами и перемещениями для каждого отдельного конечного элемента можно построить независимо, а построение соотношений для всей конструкции - отдельная процедура. Это согласуется с изложенным в разд. 2.2 и использовавшимся далее в гл. 3 и 5 подходом к расчету стержневых конструкций методом конечных элементов. Однако энергетический метод позволяет по-иному подойти к методу конечных элементов и получить глобальные соотношения, суммируя энергию отдельных элементов. Вопросы перехода от одной точки зрения к другой обсуждаются в этой и следующей главах.

Данная глава начинается с подробного изложения вывода соотношений принципа виртуальных перемещений. Далее кратко излагаются основные понятия вариационного исчисления и подробно изучаются экстремальные принципы минимума потенциальной и

дополнительной энергии. Эти принципы представляют собой специальную форму более общих принципов виртуальных перемещений и виртуальных сил соответственно. В заключение кратко рассматриваются смешанные вариационные принципы, а также гибридные и обобщенные вариационные методы построения элементов, основанные на экстремальных принципах потенциальной или дополнительной энергии.

В данной главе рассматривается только отдельно взятый конечный элемент. Все выражения записываются так, как если бы вся конструкция являлась конечным элементом, поэтому нет необходимости вводить верхние и нижние индексы, чтобы различать глобальные и локальные величины.

6.1. Принцип виртуальной работы

6.1.1. Формулировка и доказательство принципа

Принцип виртуальной работы лежит в основе следующих вариационных принципов, описываемых ниже: классических принципов стационарности потенциальной и дополнительной энергии, а также менее известных смешанных принципов. Принцип виртуальной работы, по сути дела, служит независимым подходом к построению соотношений метода конечных элементов. Используются две формы общего принципа: принцип виртуальных перемещений и принцип виртуальных сил соответственно. Они приводят к общеизвестным принципам стационарности потенциальной и дополнительной энергии.

В формулировке принципа виртуальной работы, использующей виртуальные перемещения, предполагается, что на тело, находящееся в состоянии равновесия, действуют объемные и поверхностные силы, при этом задается виртуальное (воображаемое) поле переме-

(а) (Ь)

Рис. 6.1. Сравнение допустимых и недопустимых виртуальных перемещений: (а) допустимые; (Ь) недопустимые.

щений, характеризующееся в каждой точке компонентами би, би, Ьы>. Виртуальные перемещения должны быть кинематически допустимыми, т. е. непрерьшны.ми функция.ми пространственных координат, и удовлетворять кинематическим граничным условиям на участках поверхности, где эти условия заданы.

На рис. 6.1 (а), к примеру, пунктирными линиями изображены кинематически допустимые перемещения балки. Каждое из допус-