6.1.3. Принцип согласованности при посгроении выражения для виртуальной работы

Приведенные выше построения служат прообразо.м принципа согласованности при построении конечных элементов. Очевидно, что каждая из матриц (основная матрица жесткости, матрицы массы и распределенных нагрузок) построена с применением функций формы предполагаемого поля перемещения, причем для каждой используется один и тот же набор функций формы. Поэтому матрица массы согласована с основной матрицей жесткости, и матрицы, построенные на этом принципе, называются согласованными матрицами массы.

Альтернативные виды матриц - несогласованные матрицы - появляются на практике вполне естественно. Например, при расчетах динамических задач глобальные матрицы жесткости и массы часто рассматриваются независимо. Предполагается, что массовые характеристики инерционны, поэтому можно пропорционально распределить массы для каждой из степеней свободы. Построенные таким образом матрицы массы называются матрицами сосредоточенных масс.

Подход, основанный на физической точке зрения, может быть применен и в случае распределенных нагрузок. При этом математическая модель содержит фиктивные силовые параметры {F}, отвечающие распределенным нагрузкам. Эти параметры определяются в результате приравнивания интегралов от произведений распределенных нагрузок на соответствующие перемещения к работам узловых сил на соответствующих перемещениях. Следовательно, {F} - вектор энергетически эквивалентных усилий.

Выписанные выше выражения выводятся еще раз в разд. 6.4 с помощью принципа стационарности потенциальной энергии. Затем приводятся двойственные формулировки для принципа стационарности дополнительной энергии и рассматриваются другие (смешанные) принципы стационарности. Однако сначала необходимо напомнить ряд основных положений в задаче определения стационарных значений для функций многих переменных.

Заметим, что выражения (6.12а) и (6.12е) для матриц жесткости и массы имеют вид конгруэнтных преобразований, обеспечивающих симметричность матрицы, полученной в результате умножения, если симметрична центральная матрица. Так как матрицы упругости [Е] и матрица плотности [р] симметричны, то и получаемые в результате матрицы будут симметричны. Изложенный подход отличается от прямого метода из разд. 5.1 тем, что преобразование от узловых степеней свободы к деформациям служит основой преобразования узловых сил в напряжения.

6.2. Вариационное исчисление 6.2.1. Безусловная минимизация

Принцип виртуальной работы характеризуется вариацией энергии деформации и потенциала прикладываемых нагрузок. Если рассмотреть варьируемые величины U и V, то можно установить ряд полезных свойств, которыми они обладают. Это рассмотрение показывает, что задача анализа конструкций, основанная на подсчете вариации суммы U+V, относится к хорошо разработанной области математики, известной как вариационное исчисление [6.1-6.4]. Ряд важных результатов в этом разделе математики можно непосредственно применить к задачам конечно-элементного анализа конструкций.

В этом разделе изложим некоторые наиболее простые результаты вариационного исчисления. Здесь рассматриваются непрерывные (интегральные или дифференциальные) формулировки этих результатов, перенос на дискретный случай будет осуществлен в последующих разделах. Рассмотрим сначала одномерную задачу, описываемую единственной независимой переменной А (а;), где х - пространственная координата. Основной задачей вариационного исчисления является определение величины А(х), которая доставляет стационарное значение интегралу

П=5/(, А. A)dx,

(6.19)

где A=dA/d х. Через / обозначена функция, характеризующая в механике конструкций, например, плотность потенциальной или дополнительной энергии, а П - функционал, т. е. функция от функ-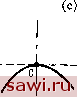

0 Д 0 Д До Д

Рис. 6.2. Типы стационарных точек: (а) минимум; (Ь) перегиб; (с) максимум.

ции (в данном случае функция от /). Стационарное значение может быть либо максимумом, либо минимумом, либо значением, отвечающим нейтральной точке. Эти случаи схематически изображены на рис. 6.2. Функция / должна быть, разумеется, дважды дифференцируемой. Если функция имеет лишь первую производную, отлич-

ную ОТ нуля, ТО она линейна, а линейные функции не имеют минимума.

Чтобы вывести выражения, позволяющие определить точку, в которой достигается стационарное значение, и иметь возможность различать представленные на рис. 6.2 ситуации, рассмотрим сначала функцию П (А), где А - переменная величина. Согласно теореме Тейлора, разложение в ряд этой функции в окрестности точки имеет вид

П(А)=П(А )+4(А-А ) + 1(А-А ) +... . (6.20)

Правило определения местоположения точки экстремума вытекает из выписанной формулы, если обозначить точку экстремума через Aq. При стремлении к этой точке расстояние А - До становится очень малым, а третий член в разложении делается пренебрежимо мал по сравнению со вторым членом. Если выполняется условие минимума, любое смещение из точки До приведет к увеличению значения П(Д), и в этом случае второй член всегда должен быть положительным. Однако, до тех пор пока производная П(До)/Д не обратится в нуль, второй член может иметь произвольный знак в зависимости от знака смещения dA. Аналогичные рассуждения справедливы и для точки максимума. Поэтому в стационарной точке справедливо следующее условие:

dn(A )/dA=0. (6.21)

Это хорошо известное требование равенства нулю угла наклона кривой в стационарной точке. В вариационном исчислении оно известно как первое необходимое условие. Стационарная точка должна удовлетворять указанному условию, однако его выполнения еще недостаточно, чтобы с уверенностью сказать, является ли эта точка точкой максимума, минимума или нейтральной точкой. Чтобы ответить на поставленный вопрос (см. рис. 6.2), необходимо определить знак кривизны (второй производной) функции 11(Ао) в точке До. В точке минимума кривизна положительна, в точке максимума - отрицательна, а в нейтральной точке - равна нулю. Символически это запишем в виде

d n (A )/dA2 > О (минимум), (6.22а)

d n (A )/dA2 < О (максимум), (6.22Ь)

dm(A,)/dA = О (нейтральная точка). (6.22с)

Вернемся теперь к вопросу отыскания стационарного значения функционала П (А). На рис. 6.3 изображена функция А в зависимости от пространственной координаты х. Предположим, что задача определена внутри интервала между точками Xi и да, а А должна удовлетворять определенным условиям в граничных точках интер-

6 л 25 47