вала; указанные граничные значения обозначим через Ai и Aj. Функция А, которая обеспечивает стационарное значение функционала Г1(А), обозначается через А и изображается сплошной линией на рис. 6.3. Чтобы определить Ао, необходимо выбрать функцию, кото-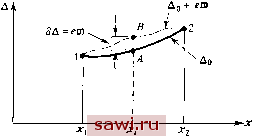

Рис. 6.3. Стационарная (Дд) и пробная (Дд-1-его) кривые.

рая отличается от Ац на величину ею, где to - произвольная амплитудная функция, удовлетворяющая условиям для А в точках х, и лга, а е - величина амплитуды. Таким образом, аппроксима-ционное выражение имеет вид

А = А + е , (6.23а)

а наклон изображенной кривой равен

dA/dx = A = A;--e . (6.23b)

Заметим далее, что его задает малую вариацию функции А, которую обозначим через 6А. Итак,

бА = е , бА=еш. (6.24а, Ь)

Вариация 6А приводит к малому изменению функционала, обозначаемому через бП, которая является первой вариацией функционала.

Символ б, или дельта-оператор, означает малые произвольные изменения зависимой переменной А при фиксированных значениях независимой переменной х. Как видно из рис. 6.3, в заданной точке Xi величина 6А есть амплитуда В - А. Отличие дельта-оператора б от оператора дифференциального исчисления dy заключается в том, что последний связывает dxc dy. Иными словами, dy характеризует расстояние по вертикали между точками данной кривой, находящимися на расстоянии dx. Важным свойством оператора дельта, используемого при построении вариационных соотношений, является коммупштивность по отношению к операциям дифференцирования и интегрирования, т. е,

(1)=( ) 6(jAd.)=J(6A)d..

Учитывая вышеизложенное, перейдем к выводу соотношений, определяющих стационарное значение функционала П. Сначала запишем функционал для аппроксимирующей функции Ао+еШ. В этом случае (6.19) имеет вид

(6.25)

Далее в этом выражении разложим / в окрестности точек Ао и Aj (при фиксированном ас). Получим

f(x, Ao + m, K + etv)-f(x, А , А;) =

(6А)+(6А)

+ члены более высокого порядка малости. (6.26)

Левая часть этого соотношения представляет собой изменение /, обусловленное вариацией 6A=eit), т. е. это б/. Поэтому, пренебрегая членами более высокого порядка малости, можно записать первую вариацию функционала в виде

6n = J6/d.=j(6A + 6A)d. = 0. (6.27)

причем приравнивание выражения к нулю сделано в соответствии с условиями стационарности.

Чтобы получить полезное выражение для бП, необходимо проинтегрировать это выражение по частям. Как показано в гл. 5, эта операция нужна частично и для того, чтобы получить граничные условия. В нашем случае интегрирование по частям поможет вынести 6А в виде сомножителя, при этом необходимо проинтегрировать по частям только второй член. Имеем

JL(6A)dx = 8A- -hA±(X)dx. (6.28)

Так как вариация 6А должна обращаться в нуль на концах Xi и Х2, первый член в правой части соотношения равен нулю. Поэтому (6.27) примет вид

6П = J6A

dx = 0.

(6.27а)

Очевидно, в силу произвольности 6А интеграл обращается в нуль при условии

d (df \ лп<и f.

или АЕ{d*u/dx)-{-q=0, которое является определяющим дифференциальным уравнением (уравнением равновесия) в этой задаче.

6.2.3. Граничные условия м ограннчения

Требования, согласно которым искомая функция или ее производная принимает заданное значение в граничных точках, известны как главные граничные условия. Если функция не удовлетворяет этим условиям, то первый член в правой части соотношений (6.28) обращается в нуль, если

а ад;=о. (б.зо)

Условие, выраженное соотношением (6.30), известно как естественное граничное условие. В качестве иллюстрации рассмотрим

Это уравнение известно как уравнение Эйлера (или уравнение Эйлера - Лагранжа) для функционала П. Функция Д, доставляющая экстремальное значение функционалу П, удовлетворяет соответствующему уравнению Эйлера. На практике величины, входящие в уравнение Эйлера, позволяют выписать определяющее дифференциальное уравнение физического процесса, описываемого исходным функционалом.

6.2.2. Пример

Чтобы проиллюстрировать, как работает выписанная выше процедура, рассмотрим функционал, отвечающий стержневому элементу. Вспомним, что виртуальная работа обусловливает равенство 6({/+V)=0. Это соответствует выполнению первого необходи.мого условия для функционала U-\-V. В случае стержневого элемента (см. разд. 5.5) имеем

L L L

U + V={-EAdx-q.udx=\\(f EA-q-u\dx.

Следовательно, сравнивая с (6.19), заключаем, что

Учитывая теперь дифференциальное уравнение Эйлера (6.29), получим ( так как здесь До=и)

а/ лр du