Заметим, что одно из полученных соотношений и есть исходное ограничение !§=0. Строгое обоснование метода излагается в книгах по вариационному исчислению (см., например, [6.1]-[6.41).

Множители Лагранжа могут иметь важный физический смысл в рассматриваемой задаче. В некоторых случаях этот смысл можно выяснить, детально изучая их свойства. В других случаях физический смысл множителей Лагранжа легко выяснить, рассматривая функционал П. Например, при расчете конструкций на основе энергетических методов П представляет собой энергию и имеет размерность силы, умноженной на перемещение. В некоторых задачах ограничения задают соотношения между перемещениями. Поэтому нз соображений размерности величина ?v должна иметь размерность силы и множители Лагранжа можно рассматривать как обобщенные силы.

стержневой элемент, для которого, согласно выписанным выше формулам, имеем dfldAa=dfldu=AE{duldx). Однако известно, что du/dx=ex, £6=0. и FAox, поэтому F=Q в этой точке. Следовательно, можно удовлетворить естественным граничным условиям, означаюш,им, что сила на свободном конце стержневого элемента равна нулю. Этому типу граничных условий в функционале энергии отвечает член, представляющий работу прикладываемых нагрузок.

В заключение важно указать способ учета ограничений, рассматриваемых в вариационном исчислении. Одним из способов является метод множителей Лагранжа. Рассмотрим задачу минимизации функционала П(Л), и пусть ограничение имеет вид

(А) = 0. (6.31)

Построим новый функционал П , называемый расширенным функционалом, умножая на константу А, и прибавляя полученное произведение к исходному функционалу:

П< = П + Я, (6.32)

где Я - множитель Лагранжа. Если теперь П достигает экстремального значения на Ао при ограничении i§(A)=0, то частные производные П по А и Я, приравненные к нулю, дадут условия для определения Ао и Я (необходимые условия)

= = 0. (6.33b)

6.3. Дискретная вариационная задача

6.3.1. Безусловная минимизация

Перейдем к изучению дискретных функционалов, в которых переменная А аппроксимируется суммой конечного числа членов. Так как рассматривается концепция метода конечных элементов, выберем аппроксимацию в виде (5.5а), т. е. А= L N J {А}. Для простоты рассмотрим случай одной переменной А. Случай, когда рассматривается поле переменных (например, А= и v w J), изучается аналогичным образом. При изучении свойств дискретного функционала полезно представить его в виде поверхности в (аг+1)-мерном пространстве, где п ортогональных координат отвечают п степеням

свободы Al, Аг.....А , а на (л+1)-й оси откладываются значения

функционала П({А}). Каждая точка на такой поверхности - значение величины П({А)). Поверхность в задаче с двумя степенями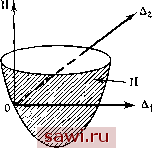

Рис 6.4. Поверхность П, задающая функционал для двустепенной системы.

свободы (Al, Aj) изображена на рис. 6.4. Нельзя изобразить ситуацию, если число степеней свободы превосходит два, однако алгебраические свойства изображенного случая переносятся и на общую rt-мерную задачу. Так как рассматриваются свойства экстремального значения П({А}), обобщим на наш случай формулу разложения в ряд Тейлора, выписанную в (6.20) для непрерывной задачи в окрестности стационарной точки {Ао}. Имеем

П({АЛ) = П({А })-ь1:1;.5д , (dA,) +

+ TEELm(dA,)+..., (6.34)

где dAj - разность между t-й компонентой {А} и соответствующей компонентой {Ао} (и аналогично для dAj). Можно также записать

an с. , ап е. , , ап

6П({А}) = -бА, + бА,+ ...+бА = {6А}=0, (6.35а)

и в силу независимости вариаций бА,

{д1УдА}=0. (6.35Ь)

Это условие применимо к i (i=l, . . п) степеням свободы А,-. В результате получим систему из п уравнений.

В некоторых случаях стационарная точка дискретизнрованного функционала обладает дополнительным свойством - это точка экстремума (максимума или минимума). Если это - точка минимума, то любое смещение из этой точки увеличит значение П. Так как \ dU/dAJ {dA} равно нулю в этой точке, то из условия минимума следует, что

L6A J[x] {6А}>0. (6.36а)

Так как вариация {6А} произвольна, выписанное условие приводит к положительной определенности гессиана [х]. По определению, матрица является положительно определенной, если для любого вектора {dA}TO произведение LdAJ[x]{dA} положительно. Для

ЭТО разложение и в матричном виде:

П ({А}) = II, + [J {dA} + LfJ [х] {dA} + . .., (6.34а)

где {dA}={A}-{Ао}, а отдельные элементы матрицы {х}, называемой матрицей Гессе, имеют вид я,у=дЧ1/дА, dAj. Как \ dIl/dAJ, так и [х], согласно (6.34), вычисляются на {Ао}. Здесь выписаны лишь три члена разложения, так как функционалы, рассматриваемые в линейных задачах механики конструкций, являются квадратичными. Поэтому производные третьего и более высокого порядка, фигурирующие в последующих членах, не дают вклада в П({А}).

Если П(А) имеет стационарную точку, то, по определению, на касательной плоскости в указанной точке выполняется условие, согласно которому любая бесконечно малая вариация координат dA, не вызовет в первом приближении изменения функционала. Это требование является первым необходимым условием, выраженным для непрерывного случая формулой (6.21) и записываемым здесь в виде

6П({А};=0. (6.35)

Чтобы преобразовать это выражение к виду, удобному для построения алгебраических уравнений, решение которых приведет к нахождению стационарной точки, используем б как дифференциальный оператор. Итак,