ТОЧКИ максимума, наоборот, справедливо

L6AJM {6Д}<0,

(6.36b)

поэтому Ы] - отрицательно определенная матрица.

Вариационная формулировка позволяет изучить вопросы, связанные с понятием согласованности в случае конечно-элементной дискретизации физической задачи. Ранее уже отмечалось, что внутри одной и той же области функция должна быть дифференцируема столько раз, каков порядок производных в соответствующем уравнении Эйлера (т. е. для стержневого элемента уравнение Эйлера имеет второй порядок, поэтому функция должна быть не менее чем квадратична). В методе конечных элементов функционал полной системы состоит из суммы функционалов Ш для р отдельных областей (элементов), т. е.

1,.... р).

(6.37)

Что же тогда может служить условием согласованности на границах элементов? Выяснить смысл этого условия поможет рассмотрение вариаций полей для одномерной полоски элементов, изображенной на рис. 6.5. Если для этого случая функционал представляет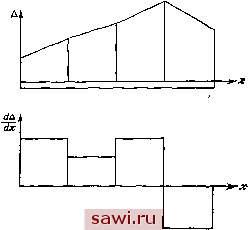

Рис. 6.5. Кусочно-постоянная вариация величины dA/dx.

собой интеграл от первой производной (dA/dx) по области, занимаемой всей системой, то видно, что непрерывность А позволяет однозначно определить П. Эта ситуация обобщается следующим образом: однозначное определение функционала возможно, если обес-

печивается непрерывность производных, на один порядок меньших, нежели наибольший порядок производных, встречающихся в функционале.

6.3.2. Метод множителей Лагранжа для учета ограничений

Метод множителей Лагранжа справедлив при наличии ограничений и в дискретизированной задаче. Если имеется г ограничений вида

;§*(Ai. .... А ) = 0 (к=\,...,г), (6.38)

со вводится расширенный функционал

П ЦА, X}} = П ({4[) -Ь 2 К , (6.39)

где второе слагаемое в правой части соотношения - сумма произведений на соответствующие множители Лагранжа 1- Приметим первое необходимое условие для каждой степени свободы Aj и для каждого множителя Лагранжа К. Система получающихся ноотношений для степеней свободы имеет вид

а дифференцирование по Я приводит к ограничениям (6.38).

Заметим, что аналогично разд. 6.2 соображения анализа размерностей позволяют определить размерности множителей Лагранжа и выявить физический смысл этих множителей. Если ;§*=0 представляют собой ограничения на перемещения, то - соответствующие силы. В гл. 7 представится возможность проиллюстрировать указанное утверждение на примере.

6.4. Минимум потенциальной энергии 6.4.1. Свойства потенциальной энергии

Принцип минимума потенциальной энергии представляет собой основу для непосредственной формулировки уравнений жесткости элемента. Потенциальная энергия конструкции Пр представляет собой сумму энергии деформации U и потенциала внешних сил V,

(6.40)

Принцип формулируется следующим образом: среди всех допустимых перемещений те, которые удовлетворяют условиям равновесия, обеспечивают стационарное значение потенциальной энергии. По-

этому

бПр = б/ + б1/=0. (6.41)

В состоянии равновесия потенциальная энергия П, минимальна. Следовательно,

&mp=8U+dV>0. (6.42)

При выводе приведенного выше принципа для простоты исключим из рассмотрения объемные силы. Обозначим через dU величину энергии деформации, приходящуюся на единицу объема, или плотность энергии деформации (см. разд. 2.4, где дается исходное определение энергии деформации). Тогда изменение плотности энергии деформации вследствие изменения величины деформации бе, вызванного виртуальным перемещение.м, равно

6(dt/)=a6e, (6.43)

где а - равновесное напряженное состояние, существовавшее до вариаций перемещений. Ввиду малости здесь опущены слагаемые, обусловленные действием приращений напряжений на соответствующнх виртуальных деформациях. Подставляя соотношения между напряжениями п деформациями (4.15), получим следующие выражения для приращения энергии деформации:

6(dt/)=8[E]6e-е [Е]б8. (6.44)

Интегрируя в пределах от О до значения е, соответствующего а, получим (меняя местами члены в подынтегральном выражении второго интеграла)

dU = г[F.]г- j е [Е] е d (vol), (6.45)

откуда для всего конечного элемента после интегрирования dU по объему имеем (обозначая третий член в правой части соотношения через С(е )):

t/ = -i- f e[E]ed(vol)- f e [E] e d (vol)-f С (e ). (6.46)

vol vo 1

Замечая также, что применение б аналогично применению дифференциала, запишем первую вариацию U в виде

6t/= j 8[E]6ed(vol)-j 8 [E]68d(vol). (6.47)

vol vol

Потенциал приложенных нагрузок равен

V=-YFA - [T-udS, (6.48)

1=1 с