Из сравнения представленных матриц жесткости видно, что для Щ построения точной матрицы требуется вычислить значение логарифмической функции, j Процедура построения профилированных балочных, пластинча-

Щ тых и оболочечных элементов на основе простой аппроксимации их геометрии аналогична описанной выше процедуре для профилированного стержневого элемента. Можно аппроксимировать гео.метри-ческие характеристики, основываясь на функциях, аппроксимирующих перемещения для элементов постоянной толщины. Этот подход называется изопаражтрическим представлением, т. е. в этом случае одни и те же (изо-) параметры используются для аппроксимации перемещений и геометрии. Степень непрерывности полей перемещений при переходе от одного элемента к другому, заложенная в функциях формы, переносится и на геометрическое представление. Так, в рассматриваемом выше примере функция (площадь) непрерывна при переходе от одного элемента к другому. Общая теория изопараметрического представления будет изложена в разд. 8.8.

В практике проектирования не прижились даже столь простые способы аппроксимации профилированных стержневых и пластинчатых элементов. Проектировщики предпочитают использовать сту пенчатую аппроксимацию элементами постоянной толщины. Вообще говоря, имеющиеся в настоящее время вычислительные возможности позволяют достаточно точно аппроксимировать очертания подобного рода конструкций, используя большое число элементов. Поэтому подходы, использующие изопараметрические представлен ния, еще не получили широкого распространения при расчетах профилированных элементов. Однако это не так в случае трехмерных тел, когда расчеты даже на относительно грубой сетке конечных элементов требуют очень больших вычислительных затрат.

Альтернативой использования профилированных элементов яв ляется непосредственное численное интегрирование и подсчет интеграла энергии деформации. При этом во всех точках численного интегрирования должны быть затабулированы значения геометрических характеристик, входящих в подынтегральное выражение, и, естественно, этот подход применим также для интегралов, возникающих в описанных выше процедурах (изопараметрическое представление). Действительно, получаемое, согласно изложенному в разд. 8.8 подходу, использующему изопараметрическое представление, подынтегральное выражение в интеграле энергии деформации обычно бывает слишком сложным и поэтому для его интегрирования требуется привлекать численные методы.

6.5. Гибридные методы перемещений и метод обобщенной потенциальной энергии

6.5.1. Первый гибридный метод перемещений

Предлагаемые гибридные методы перемещений и метод обобщенной потенциальной энергии являются альтернативами методов, использующих единственное аппроксимирующее поле и характеризующихся межэлементной согласованностью. Как гибридные методы, так и метод обобщенной потенциальной энергии базируются на применении нескольких полей, когда одно поле перемещений задано внутри элемента, другое поле перемещений или напряжений определено независимым образом на границах элемента. В гибридном методе уравнения для элемента выводятся в результате исключения обобщенных параметров, а в методе обобщенной потенциальной энергии подправляются несоответствия в перемещениях вдоль границ элементов, образовавшиеся в результате использования полей, характеризующихся межэлементной несогласованностью.

В этом разделе изучаются два гибридных метода, основанных на рассмотрении функционала потенциальной энергии. В первом из них (гибрид I) поле перемещений внутри элемента выражается в терминах обобщенных перемещений, а поле напряжений на границе описывается независимо в терминах узловых сил. В результате получается .матрица податливости элемента. Второй метод (гибрид II) основывается на предложенной выше концепции в том смысле, что поле перемещений внутри элемента и граничные напряжения выражаются в терминах обобщенных параметров, а перемещения на границе независимо описываются с помощью узловых перемещений. Это приводит к матрице жесткости элемента.

Для того чтобы оперировать с независимыми полями, необходимо модифицировать выражение для потенциальной энергии. Описывая модификацию, используемую в гибридном методе I, рассмотрим лишь внутренние элементы, т. е. элементы, стороны которых не лежат на границе конструкции, и исключим из рассмотрения объемные силы и начальные напряжения. Под границей элемента понимается совокупность всех сторон элемента (S ) и считается, что на границе действуют межэлементные усилия Т. Поэтому, согласно (6.40) и (6.49), имеем модифицированное выражение для потенциальной энергии

Щи- Jf-udS, (6.54)

где U - граничные смещения, согласующиеся с выбранным полем перемещений внутри элемента А. Обобщение известного выражения для потенциальной энергии заключается в том, что Т запишется в терминах узловых силовых параметров. Поэтому как параметры

перемещения и (и А), так и силовые параметры в узлах будут играть роль неизвестных в П. В классической формулировке принципа минимума потенциальной энергии в выражения входят лишь параметры перемещения. Для того чтобы выяснить, как описываются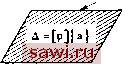

и = М1а}

Р,{типичная)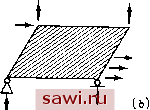

Рис. 6.8. Предполагаемые поля напряжений и перемещений, используемые в первом гибридном методе перемещений, (а) Описание перемещений (внутренние и поверхностные перемещения выражены через одни и те же обобщенные параметры {а}); (Ь) описание перемещений (поверхностные силы выражены через силы, заданные в узлах, которые могут свободно смещаться).

ПОЛЯ внутри элемента и на его границе, на рис. 6.8 приведен гипотетический элемент и изображены предполагаемые поля перемещений и напряжений.

Согласно используемой в гл. 5 терминологии, обозначим обобщенные параметры внутреннего поля перемещений через {а}. Для обычного полиномиального представления имеем

А=[р] {а}, (5.2а)

и используя соотношения между перемещениями и деформациями, приходим к соотношению

е=[Су] {а}, (5.6d)

где через {а} обозначены степени свободы, которые остались после того, как в результате выполнения операций дифференцирования в формулах, связывающих перемещения и деформации, были исключены степени свободы {а}, отвечающие движению тела как твердого целого. Кроме того, требуется рассмотреть граничные значения и этого поля. Указанные величины получаются непосредственными вычисления.ми значений Л вдоль границы элемента. Имеем

u = [Y]{a} = [Y, Y,l{j,

(6.55)

где для удобства дальнейших рассуждений выделены степени свободы {а} и {а}.

Последней существенной частью гибридного метода перемещений является вопрос о записи граничных усилий Т через узловые силы {F/}. Нижним индексом / помечена система узловых сил, в