полнительной работы. Обратите матрицу податливости и получите соответствующую матрицу жесткости.

6.18. Постройте матрицу податливости трехузлового треугольного элемента для плоского напряженного состояния, используя принцип минимума дополнительной работы. Используйте условия закрепления Ui=V2=Vg=Q (см. рис. 5.3). Сравните результат с матрицей податливости из задачи 2.4.

6.19. Пользуясь принципом минимума дополнительной работы, постройте матрицу податливости для изгибаемого криволинейного элемента, изображенного на рис. Р6.19. Сравните с матрицей, приведенной в задаче 2.6. (Крепление в точке 2.)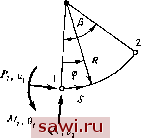

Рис. Р6.19.

6.20. Прн помощи гибридного метода напряжений постройте матрицу жесткости треугольного элемента, находящегося в плоском напряженном состоянии (рис. 5.3), используя для этого постоянное поле напряжений и линейное распределение перемещений на границах. Сравните результат с рис. 5.4.

6.21. Выпишите функционал Рейсснера в дискретном виде, используя значения функции напряжений Эри как параметры напряжений, а также компоненты перемещений U и у. Обсудите выбор вида функций формы для этих полей в случае четырехугольного элемента с узлами в вершинах четырехугольника.

ВАРИАЦИОННЫЕ ПРИНЦИПЫ ГЛОБАЛЬНОГО АНАЛИЗА КОНСТРУКЦИЙ

Применение вариационных принципов при формулировке соотношений для элемента позволяет, как показано в гл. 6, построить соотношения податливости, жесткости и смешанные соотношения. С помощью процедур из гл. 3 полученные таким образом соотношения жесткости можно непосредственно использовать для построения уравнений, описывающих поведение всей конструкции. Таким образом, может показаться, что вариационные принципы не потребуются в дальнейшем, кроме как для построения соотношений, описывающих отдельный элемент. В действительности же вариационные принципы чрезвычайно полезны и в некоторых вопросах глобального анализа конструкций.

Прежде всего, вариационные принципы позволяют предложить различные подходы к построению глобальных уравнений. При глобальном анализе конструкций роль вариационных принципов во многом заключается в том, что они позволяют с другой точки зрения взглянуть на алгебраические операции, обусловленные различными подходами. Специальным операциям глобального анализа можно также дать вариационную трактовку; вариационный подход особенно важен при учете ограничений по методу множителей Лагранжа. Кроме того, на вариационных принципах основаны методы доказательства сходимости, а некоторые из этих принципов позволяют даже установить характер сходимости.

Далее подробно исследуется метод, основанный на принципе минимума потенциальной энергии, и рассматривается метод, базирующийся на принципе минимума дополнительной работы. Смешанные методы не рассматриваются, так как для них процедуры построения глобальных уравнений аналогичны процедурам, основанным на обычных вариационных принципах. Для этих методов не установлены свойства сходимости, которые позволили бы определить верхнюю или нижнюю границы для точного решения.

7.1. Принцип минимума потенциальной энергии

Чтобы объяснить, как применяют метод, основанный на принципе минимума потенциальной энергии, для глобального анализа конструкции, опять напомним, что энергия деформации - скалярная величина. Поэтому энергия деформации U для всей конструкции, состоящей из р элементов, равна сумме р слагаемых, представляющих энергию деформации отдельных элементов, т. е.

= Xt=4-XLAJ[k]{Ab (7.1)

1=1 <=i

где L J и [ll - соответственно вектор узловых перемещений и матрица жесткости г-го элемента. Чтобы использовать это обстоятельство при построении глобальных алгебраических уравнений, введем следующие массивы;

{А}= L L J L J . .\ Ар } \ - вектор, содержащий все наборы степеней свободы; определен ранее в (3.12). (7.2)

[ J - несвязанная глобальная матрица жесткости. Эта матрица блочно-диагональная, каждый блок которой - матрица жесткости элемента. Все матрицы жесткости элементов включены в этот массив. Матрица L1<*J была введена в разд. 3.3 согласно формуле (3.13).

С учетом этих обобщений выражение (7.1) можно записать в виде

(/=V,LAJ ГкЛА}- (7.3)

Теперь необходимо учесть, что элементы соединены. С этой целью обратимся опять к содержанию разд. 3.3 и уравнения (3.14), т. е. {A*}=[i4]{A}. Здесь {Л} включает все глобальные перемещения в узлах, а матрица [А], как отмечено ранее,- глобальная матрица связности. Применяя е& к U в виде классического преобразования, получим

y=(LAJ/2)[K]{A}. (7.4)

где [K] = [/llTk*Jll. (7.5)

Матрица [К1 полностью совпадает с глобальной матрицей жесткости, построенной в разд. 3.3. Там же приводится и численный пример, иллюстрирующий изложенную выше процедуру.

В разд. 3.3 утверждалось, что матрицы жесткости элементов, включающие Г J, не должны содержать степени свободы, отвечающие движению тела как твердого целого. Это можно объяснить теперь с энергетической точки зрения следующим образом. Матрица [к] для каждого элемента строится в соответствии с определением энергии деформации. Поэтому, как указывалось в разд. 2.4, энергия деформации элемента полностью определяется