Правильное решение равно, конечно, /s{PtL/AE), для которого

Пр=-7з(Р11М£).

Если требуется описать поведение потенциальной энергии в более общих случаях, например когда рассматривается большое число степеней свободы, то необходимо ввести по одной ортогональной

Рис. 7.1.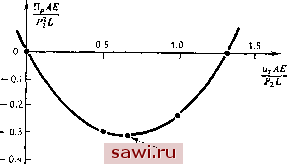

Точное решение

Рис. 7.2.

ОСИ для каждой степени свободы и дополнительную ось для Пр. Невозможно изобразить указанную ситуацию для более чем двух степеней свободы, однако указанные геометрические свойства используются в подходе, кратко описанном в конце разд. 7.1.

Рис. 7.3.

Чтобы показать важность теоремы о нижней границе при выборе пол перемещений для отдельных элементов, рассмотрим сужающийся стержневой элемент, изображенный на рис. 7.3. Точное поле и в этом случае есть логарифмическая функция, однако в разд. 6.4

при построении соответствующих коэффициентов жесткости использовалось линейное поле, применимое для элементов постоянного поперечного сечения, т. е.

Рассмотрим случай, когда площадь поперечного сечения на правом конце элемента в два раза больше площади сечения на левом конце. Если левый конец стержня неподвижен, то в точном решении смещение 2, соответствующее единичному значению Fj, равно

2 = 7T-Vtp In f ф) = 0.69315 {At - Ai)E AiJ Л,£

С другой стороны, приближенное решение равно

Таким образом, приближенное решение примерно на 4% меньше точного решения. Образуя конечно-элементные представления стержня

Готое решение

0.690

Приближенное решение, являющееся нижней границей

Рис. 7.4.

3 Число элементов

С различным числом конечных элементов, получим сходимость к точному решению, как показано на рис. 7.4.

7.3. Учет ограничений методом множителей Лагранжа

Как показано в разд. 6.2, метод множителей Лагранжа является подходом, позволяющим учесть ограничения (связи) в рамках классических представлений вариационного исчисления. Применим

ЭТОТ метод к системам со многими степенями свободы. В этой форме указанный метод является альтернативой к описанному в п. 3.5.2 методу преобразований.

Согласно концепции метода множителей Лагранжа, экстремум функционала при ограничениях (связях) может быть найден, если у.множить каждое ограничение на константу (.j- множитель Лагранжа), прибавить полученные выражения к исходному функционалу и выполнить варьирование по каждой степени свободы и каждому множителю. Как и ранее (см. (3.28)), для г связей и п степеней свободы система в общем виде записывается следующим образом;

101.х {А}пХ1 = {8}лхх. (7.16)

При этом г величин ki обозначим через

1к \ = 1К..Л,...Хг- (7.17)

Теперь, согласно принятой выше методике, построим вспомогательный функционал Щ:

n? = 4-[K]{A}-LAJ{P}+LM[G]{A}-LJ{s}- (7.18)

Варьируя по каждой и Я, получим следующую систему уравнений:

Заметим, что в нижней части матричного соотношения записана система ограничений. Эти уравнения можно решить непосредственно. Матрица, определяющая эту систему, положительно полуопределена. Поэтому, выбирая алгоритм решения, нужно быть осторожным. В предположении, что матрица [К] неособая, из решения верхней части уравнений получаем

{A}=[K]-i{P}-[K]-4G]T{>.}, (7.20)

поэтому из нижней части находим

{k}=(lG\ IKJ-MG] )-4lGl [K]-4P}-{s}), (7.21)

откуда, подставляя полученное выражение обратно в (7.20), находим {А}.

Следует отметить, что (7.19) отвечает формулировке смешанного типа. (Ср. с (2.3).) Это можно понять, вспоминая, что согласование размерностей в расширенном функционале приводит к тому, что множители Лагранжа имеют размерность силовых параметров. Ввиду положительной полуопределенности соотношений (7.19) не удается доказать в общем случае, что найденное таким образом решение, основанное на принципе минимума потенциальной энергии, дает нижние границы для рассматриваемых характеристик.