Следует также заметить, что в методе преобразований из п. 3.5.2 матрица преобразований [Г1 вначале используется в функционале для потенциальной энергии, а затем преобразованная величина Up варьируется по оставшимся степеням свободы. Это иллюстрируется на рис. 7.5, где изображена показанная ранее на рис. 6.4 по-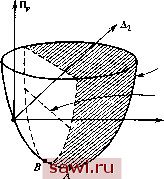

Ограничение С(Л1,Лг) = 0

Рис. 7.5. Поверхность П, задающая потенциальную энергию двустепенной системы, при наличии ограничения G(Ai, Д2)=0.

верхность, соответствующая потенциальной энергии системы с двумя степенями свободы (Ai и Aj). В данном случае имеется линейная связь G(Ai, А2)=0. Эта связь определяет плоскость, перпендикулярную к плоскости Al, Аа и отрезающую участок поверхности, изображающей энергию, на котором находится точка минимума А для предыдущего случая. Теперь минимум достигается в точке S, находящейся на кривой, полученной в результате пересечения поверхности плоскостью.

Метод преобразований уменьшает число входящих в систему уравнений, а метод множителей Лагранжа увеличивает. Однако следует иметь в виду, что метод преобразований требует значительного числа матричных операций.

Рис. 7.6.

Чтобы проиллюстрировать метод множителей Лагранжа, рассмотрим изображенную на рис. 7.6 систему, состоящую из стержневых элементов, при ограничениях - =0. Согласно методу

множителей Лагранжа, имеем систему уравнений {ко=АЕ/1) 2к, -к, V

-I О

Решая эти уравнения путем обращения матрицы, получим

Условие U2=us предполагает наличие жесткого элемента между точками 2 и 3, поэтому упруго деформируются лишь звенья А и С. Таким образом, как следует из анализа решения, смещение точки 2, вызванное действием силы Pj, равно Pj2ko. Это же значение для смещения получается, если действует лишь сила Рз. Множитель Лагранжа =/2(2+3) - силовой параметр; в этом случае он соответствует силе, передаваемой через жесткое звено. Заметим, что связи наложены на закрепленную конструкцию. Поэтому здесь может быть применена процедура (7.20), (7.21), в которой обращается базисная матрица жесткости.

Условия закрепления A,-=0, являющиеся одновременно ограничениями, можно также учесть с помощью метода множителей Лагранжа. Обычно (см. разд. 3.2) это осуществляют путем непосредственного вычеркивания из матрицы жесткости столбцов, отвечающих этим условиям, и исключением из матрицы соответствующих строк. Однако в подходе, использующем множители Лагранжа, глобальную матрицу жесткости можно оставить без изменений.

Рис. 7.7.

если к выражению для потенциальной энергии добавить умноженные на множители Лагранжа члены, соответствующие каждому условию закрепления. Эту процедуру можно проиллюстрировать на примере стержневого элемента, изображенного на рис. 7.7. Элемент закреплен на левом конце так, чтобы i=0. Система алгебраических уравнений, отвечающая методу множителей Лагранжа, в

ЭТОМ случае имеет вид

г АЕ -АЕ р

-АЕ L 1

О 0J

Если поменять местами первый и третий столбцы выписанной вспомогательной матрицы жесткости, то придем к легко разрешимой системе уравнений, откуда получим

откуда в свою очередь Ua-FL/AE, Ui=0 и A,=Fi+/a. В этой задаче множитель Лагранжа равен сумме сил, действующих в направлении оси X. При этом ограничения накладываются на незакрепленную конструкцию, что приводит к вырожденности основной матрицы жесткости. Следовательно, процедуру, представленную соотношениями (7.20) и (7.21), здесь применить нельзя.

7.4. Метод обобщенной потенциальной энергии

В гл. 6 изучался ряд подходов, альтернативных к традиционным и основанных на принципах минимума потенциальной и дополнительной энергии. Причем альтернативные подходы характеризовались смягчением условий непрерывности полей между элементами. Изложенные процедуры позволяли сформулировать для элемента самосогласованные соотношения, которые стыкуются с соотношениями соседних элементов, не требуя введения модификации в процедуру глобального анализа. Ниже описывается другой класс процедур, в которых условия на межэлементную непрерывность полей смягчены, но для реализации которых требуется выполнить специальные операции с глобальными уравнениями (и, в частности, наложить некоторые ограничения на глобальные уравнения жесткости).

В излагаемом подходе предполагается, что пробные функции для элемента записываются в терминах степеней свободы в узлах соединений, т. е. А= L N J {А}. Считаем также, что степени свободы {А} связываются с соответствующими степенями свободы соседних элементов, а пробные функции не полностью совместимы на границах, разделяющих элементы. Предположим, к примеру, что смещения и вдоль стороны 1-2 изображенных на рис. 7.8 элементов А