И В описываются функциями

uf i = Nfu, + NfUi + Nu, + Ntu uf i = Nfu, + Nu, + yvf+ yvf

(7.22a) (7.22b)

где Nf, . . ., Nb-квадратичные функции от у (вообще говоря, указанные функции зависят oi х и у, однако здесь они вычисляются вдоль линии, на которой х не меняется). Ни для элемента А, ни для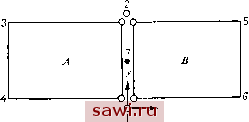

X, и

Рис. 7.8.

элемента В перемещение не определяется однозначно заданием перемещений щ и в концевых точках. Величины и и uf 2 на границе 1-2 различны; следовательно, перемещения терпят разрыв и существует невязка uf-uf 2. Однако межэлементная непрерывность может быть восстановлена при помощи задания условия

\{ut-ut,)dy = 0.

(7.23)

левая часть которого с учетом (7.22) преобразуется к виду

С [{Nt - Nf) u, + (Ni- /Vf) 2 + Niu, + Niu, - Nfu, - Nfu,] dy. 0 (7.24)

После интегрирования получим линейное алгебраическое уравнение вида

Gu i+Gi2 2+Gi3 3+Gi4U4+Gi,u,+GieU,=0. (7.25)

Используя методы множителей Лагранжа, можно учесть уравнение (7.25) в процессе решения. В рассматриваемом примере для каждой компоненты смещения на каждой из границ элемента возникает по одному такому соотношению.

В данном случае множители Лагранжа представляют среднее значение внутренних сил на линиях, вдоль которых устраняются разрывы полей перемещений. Более того, глобальные уравнения имеют вид уравнений (7.19), которые представляют собой соотношения между силами и перемещениями в смешанной формулировке (см. уравнение (2.3)). Таким образом, смешанные формулировки

Следует заметить, что альтернативный подход к определению ограничений, восстанавливающих непрерывность, заключается в обеспечении непрерывности в дискретных точках границы. В приведенном выше примере имеется невязка для одной степени свободы в полях перемещений на границах элементов. Обозначая точку, лежащую на стороне 1-2, цифрой 7 (см. рис. 7.8), можно записать uf-uf=0. Вычисляя затем в точке 7 соответствующие значения полей перемещения для элементов А п В, получим уравнения, задающие ограничения в виде, аналогичном соотношению (7.25). Если учесть указанное ограничение с помощью метода множителей Лагранжа, то в этом случае множитель Лагранжа представляет собой величину силы в рассматриваемой точке.

Преимущества обобщенного вариационного подхода отчетливо проявляются при построении конечно-элементных моделей изгибаемых пластин. Возможность проиллюстрировать этот факт представится в гл. 12.

МОЖНО интерпретировать как результат применения традиционных энергетических методов со смягченными требованиями непрерывности.

Если разрыв полей перемещений вдоль каждой из границ, разделяющих соседние элементы, более высокого порядка, то на каждой такой границе требуется ввести дополнительное уравнение-ограничение. Один из способов учета этих ограничений состоит в требовании, чтобы невязки из-за разрывов вдоль границы равнялись нулю. Для этого выпишем произведение функции, задающей ограничения, на множитель Лагранжа А,(и 2-uf 2)=0, где К - в нашем случае непрерывная функция координаты, меняющейся вдоль границы. Затем прибавим к выражению для потенциальной энергии

член Х{и 2- f-2) dy. Чтобы на основе выписанного функционала системы получить алгебраические уравнения, разложим X в степенной ряд ХХ+Ху {-Xy-i-. . ., выбирая столько членов, сколько имеется условий, необходимых для однозначного определения перемещения вдоль стороны. Поэтому имеем

Х{и 2- f-2) dy = X j {uf 2 - f 2) dy + Xi {u ,-uf 2) ydy +

+ X2{ut2-ut2)ydy+...,

так что ограничения принимают вид

f ( .- f 2)dy = 0, f {ut.-uf-d ydy = 0,

(7.26)

(ut, - 4?2)ydy0.....

7.5. Принцип минимума дополнительной энергии

Если при конечно-элементном анализе в соотношениях податливости в качестве неизвестных выбрать узловые или граничные силы, то выписать соответствующие формулировки на базе выражения для дополнительной энергии намного труднее, нежели конечно-элементные представления жесткостной формулировки, опирающиеся на принцип минимума потенциальной энергии. Это происходит из-за того, что для статически неопределимой конечно-элементной идеализации конструкции нельзя непосредственно выполнить преобразование от узловых сил элемента {F} к прикладываемым нагрузкам {Р}. Если, с другой стороны, в качестве основных неизвестных выбраны функции напряжений, то формулировки сходны с используемыми при жесткостном представлении. Опишем эти два подхода ниже.

Рассмотрим вначале случай, когда в качестве неизвестных выбираются силы, причем объемные силы и предварительные напряжения предполагаются отсутствующими. Для определения величины дополнительной энергии деформации U* в конечно-элементной модели, состоящей из Р элементов, воспользуемся соотношением {6.68Ь). Имеем

и*=Х = TiLFJ[f]{Fb (7.27)

1=1 i=i

где {F} и (f} - соответственно вектор сил и матрица податливости i-ro элемента. Это можно записать в следующем виде:

U*4ilFJUJ{F}, (7.28)

где {F*} - вектор, включающий всю совокупность силовых векторов отдельных элементов \ F J и все силы реакции опоры L J.

LFj = L LFj LFJ ... LFJ LR J-

Здесь LfJ - глобалбмая матрица податливости, имеющая блочно-диагональную структуру, где каждый блок есть матрица податливости отдельного элемента. Все матрицы отдельных элементов [f], t = l..... р, входят в этот массив. Кроме того, в нем фигурируют нулевые строки и столбцы, соответствующие силам реакции опоры в точках закрепления.

Может показаться, что следующий логически оправданный шаг состоит в переходе от внутренних сил и сил реакции {F} к узловым силам {Р}; однако, как было указано выше, это нельзя осуществить непосредственно в случае статически неопределимой конструкции. Следовательно, {F*} выражается в виде суммы двух силовых систем {F } и {F}. Здесь {F } - любая система внутренних сил, уравновешивающих {Р}, и пока выбор этой системы не соответствует