функции формы следующим образом:

+ N Ai + Л. + Л + + Л2.ДГ. (8-14)

где верхние индексы у Ai и (например, т -1) означают порядок производных по X. Теперь в нашем распоряжении имеется 2т. условий для построения каждой функции формы vV; , так как каждая функция формы (или ее соответствующая производная) должна равняться 1, если А (или ее соответствующая производная) вычисляется для степени свободы, отвечающей Ль и должна равняться нулю, если вычисления проводятся для любой из оставшихся {2т-1) степеней свободы. Следуя принятому в практике выбору полиномиального описания функции поведения, заключаем, что существование 2т условий предполагает описание каждой функции vV; полиномом порядка 2т-1, т. е. полиномом, имеющим 2т коэффициентов. Таким образом,

Niax+a2l+asl+ . . . +a2mE= -. (8.15)

Далее разрешаем полученные выражения относительно 2т величин а,-. Указанные операции повторяем для каждой из 2т функций формы Л;.

Вышесказанное можно проиллюстрировать на примере простого изгибаемого конструктивного элемента, изображенного на рис. 8.6. Так как предполагается, что на каждом конце поперечное перемещение ш и его первая производная непрерывны, то т=2. Здесь а=ш и в точке 1

А = щ, а; = -[ = 9,.

Аналогичные равенства справедливы и для точки 2. Из (8.15) следует, что каждая функция формы в этом случае имеет вид

Рассмотрим теперь построение функции Ni. Вначале представим ее в виде М1=а1+а21+аз1+а1. Полагая Ai=l при х=0 и vVi=0 при x=L, а N[=0 на обоих концах х=0 и x=L, получим

1 =1 (Л1 = 1 при 1 = 0),

0 = (Л; = 0 при Е = 0),

0 = (а,+а, + а, + а,) (УУ = 0 при Е = 1), = Т + П + ПГ (1 = 0 приЕ=1).

откуда 1=1, 2=0, аз=-3, 4=2, поэтому yVi=l-3?+2. Аналогичным образом находим, что оставшиеся функции формы, задаваемые первоначально с помощью (5.14а), имеют вид

yV3=3=-2E3 М=-х(1-\у, N,=-x(l--l).

8.4. Прямоугольные элементы

Чтобы обобщить концепцию интерполяции на двумерный случай и построить функции, которые однозначно определяются на каждой стороне прямоугольника с помощью заданных на этих сторонах и вершинах прямоугольника степеней свободы, можно использовать простое перемножение одномерных в направлениях х и у функций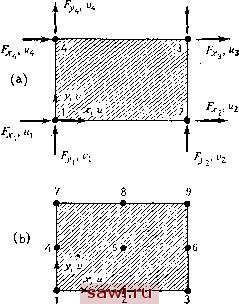

Рис. 8.7. Интерполяция Лагранжа в двумерном случае, (а) Прямоугольник с билинейной функцией; (Ь) прямоугольник с биквадратной функцией.

форм. Изображенный на рис. 8.7(a) прямоугольник с узлами, расположенными только в его вершинах, для которого требуется найти линейное поле перемещений, служит примером указанной процедуры. Имеем для компоненты перемещений А (которая может быть и или у):

A-{NixNiy)Ai+{N,xNiy)K+(N2xN,y)A,+iNixN,y)A (8.16)

A=L(i-l)IJ

l(l-ri)

что приводит к (8.16).

в разд. 8.5 при помощи треугольника Паскаля демонстрируется, что не представляет труда задать совокупность узлов для треугольных элементов, обеспечивающую полноту полиномиальных разложений вплоть до любого заданного порядка. Чтобы выяснить взаимосвязь между лагранжевой интерполяцией для прямоугольных элементов и полнотой соответствующего полинома, рассмотрим вновь изображенный на рис. 8.8 треугольник Паскаля.

Во-первых, следует заметить, что порядок одномерного полинома в точности отвечает соответствующему порядку интерполяционной формулы Лагранжа. Например, A=ai+a2X соответствует линейной интерполяции. Тогда билинейная интерполяция, определенная в терминах обобщенных координат, может быть описана на основе треугольника Паскаля в виде произведения линейных функций. Из рис. 8.8(a) следует, что это приводит к Д=а1-Ь -{-ах+азу+аху. Коэффициенты полинома при биквадратной ин-

** Здесь и в других примерах этой главы способ нумерации узлов, описанный в разд. 2.1, не используется.

где Nix={\-1), N2x=l, Л1!,=(1-Tl), Nty=r\, а l-=x/x2, Ц=у1уз. Соотношение (8.16) отвечает билинейной интерполяционной формуле.

Далее можно рассмотреть изображенный на рис. 8.7(b) ** прямоугольник, имеющий дополнительные узлы на серединах сторон и один узел внутри элемента (биквадратная интерполяция). Имеем

Д = {N,xN,;) Д, + {N,x N,y) Д, + {N,x N,y) \ +

+ (N N J Д, + (N N,y) Д, + (yv N,y) Д, +

+ {N yV3,) Д, + {N yV,) Д, + (N,x N,y) Д (8.17)

где Nix=[{x-2x2) (x-Xi)]/2xl и т. д. согласно введенной ранее лагранжевой процедуре интерполяции.

Заметим, что полная интерполяция квадратичной или более высокого порядка функции приводит к появлению внутренних узлов. Интерполяция кубической функции дает массив размерности 4x4 и четыре внутренних узла.

Указанные выше построения легко провести, вводя следующее тройное матричное произведение:

A=LNJ L?J(N}. (8.18)

где L J , L J - векторы функции формы соответственно в направлениях X м у, а [R\ ~ матрица узловых перемещений. Для билинейной интерполяции, например, имеем