8.5. Треугольные элементы

В случае треугольных элементов процедуры интерполяции тесно связаны с понятием треугольных координат. Эти координаты помогают не только построить функции формы, которые непосредственно относятся к узловым, а не к обобщенным степеням свободы, но также с их помощью регулярным способом обозначить узловые точки элемента. Другие преимущества использования треугольных координат становятся очевидными только после детальных рассмотрений.

Грань 1 / I \Грань 1

Рис. 8.12. Треугольные координаты.

Регулярный способ обозначения узлов в треугольных координатах может быть задан, как указано на рис. 8.12. В этом случае грани элемента определяются противолежащей вершиной. Например, грани 1 противолежит вершина 1. Исследуем сначала способы идентификации узла внутри треугольника. Если, как указано на рис. 8.12,

жение входит 16 членов. Данная функция формы изучается еще раз более подробно в разд. 12.2.

В зависимости от задачи необходимо определить различное число узлов на каждой из четырех сторон или же иметь одинаковое число узлов на каждой стороне, но исключить внутренние узлы. Если можно в каждом из случаев выделить соответствующие члены полиномиального разложения, то легко построить преобразование от обобщенных параметров полинома {а} к узловым перемещениям {А}, а затем с целью получения выражений в терминах последних разрешить эти соотношения (см. (5.3а) - (5.5а)). Внутренние узлы можно исключить, задавая полную интерполяционную функцию, выписывая энергию деформации для элемента и конденсируя нежелательные степени свободы с помощью процедуры, описанной в разд. 2.8. Альтернативным подходом служит непосредственное построение функций формы с помощью методики, обсуждаемой в разд. 8.7.

Обращая матрицу, получим

1 = Фо. + ЬгХ + Ь2.у) (/ = 1,2,3), (8.22)

(8.23)

индекс i пробегает значения 1, 2, 3, и

А=Ч2(х2Уз+ХзУ1+Х1у-Х2Ух~ХзУ2-Х1Уз). (8.24)

Здесь Л, согласно обозначению,- площадь треугольника.

провести ИЗ данного узла внутри треугольника отрезки к его вершинам, то исходный треугольник разделится на три треугольника с площадями Ai, Аи A3, где нижние индексы соответствуют прилежащим граням. Треугольные координаты Li{i=\, 2, 3) суть по определению отношение площадей Ai ко всей площади А, т. е.

U=AJA, L2=AJA, Lз=Л,/Л. (8.19)

Кроме того, сумма указанных площадей равна А: Ах-\-Аа-\-Аь= =А. Разделив обе части соотношения на А, получим

Li+L2+L3=l. (8.20)

Очевидно, что, согласно п. 8.3.1, эти координаты являются естественными координатами треугольной области. Теперь треугольные координаты можно использовать для определения прямоугольных координат хну изображенной на рис. 8.12 точки. Имеем

x=LiXi+L2Xi+L3X3, у=иу1+12У2+Еяуз. (8.21)

Справедливость этого утверждения можно легко проверить. Действительно, предположим, что точку перемещают внутри треугольника до тех пор, пока она не совпадет с точкой 1. Тогда Ai=A, Л 2=Л 3=0 и Li=l, L2=L3=0. Следовательно, если х соответствует точке 1, то x=Xi. Очевидно, что треугольные координаты полностью совпадают с функциями формы для простого треугольного элемента с тремя узлами.

Геометрические характеристики элемента заданы с помощью координат вершин хну. Чтобы выразить Li, и Ls через эти данные, объединим (8.20) и (8.21) в следующую систему из трех уравнений;

Если сторона, соединяющая точки 1 и 2, расположена вдоль оси X и точка 1 помещена в начале координат {хх=У\=У2=0), то получим

-1 =

Ч Уз 1

(хУз-хуа-ху + ХаУ), (хУз-ХзУ), -

Уз

Эти члены совпадают с функциями формы Ai, N, N 3, заданными посредством (5.21а) для идентично расположенного треугольного элемента постоянной деформации.

Для того чтобы построить функции формы для элементов высокого порядка в треугольных координатах Lj, необходимо вначале определить способ задания и обозначения узлов указанных элементов. Эти рассуждения проиллюстрированы на рис. 8.13. Стороны

Грань 0

Вершина

Вершина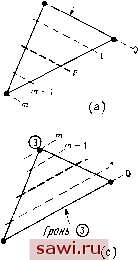

Рань ф.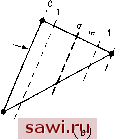

вершина ©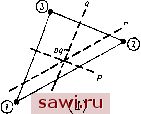

Рис. 8.13. Нумерация узлов сетки для треугольных координат, (а) Сетка в направлении 1; (Ь) сетка в направлении 2; (с) сетка в направлении 3; (d) обозначение типичного узла pgr.

обозначаются по противолежащей вершине, например сторона 1 лежит против вершины 1. Нормаль к стороне определяет соответствующее направление. Штриховые линии на рис. 8.13(a) делят расстояние между стороной 1 и узлом 1 на т равных сегментов в направлении 1. Каждая линия пронумерована цифрами от О до т, причем линия с номером О совпадает со стороной 1. [Эти узлы не нумеру-