ются целыми числами от 1 до т+1, см. рис. 8.3(a), так как предыдущая нумерация более удобна. Аналогичный сдвиг при нумерации был проведен в одномерном случае на рис. 8.3(b).] На рисунке типичная линия разбиения обозначена символом р. Указанное разбиение приводит к появлению (m-f 1) узлов на сторонах 2 и 3 и, очевидно, создает предпосылки для построения поля перемеще-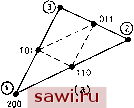

@ 003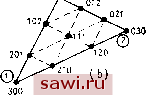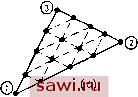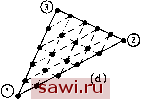

Рис. 8.14. Треугольники высокого порядка (а) Полный квадратичный полином (т=2); (Ь) полный кубический полином (т=3); (с) полный полином четвертого порядка (т=4); (d) полный полином пятого порядка (т-Ъ). 1, 2, 3 - вершины, соответствующие треугольным координатам L-i, L, L3

НИИ, основанного на полиномиальном представлении т-го порядка. Аналогичные построения можно провести для направлений 2 и 3, как показано на рис. 8.13(b) и (с), где типичные линии обозначены соответственно через q и г.

На рис. 8.13(d) показан способ идентификации некоторого узла. Узел задается тремя цифрами р, q н г ъ соответствии с обозначением типичных линий в трех направлениях. Заметим, что сумма трех чисел (p+q+r) равна т. Указанный способ идентификации точек иллюстрируется на рис. 8.14 для четырех видов разбиения треугольного элемента. Следует заметить, что узлы в вершинах также помечены цифрами 1, 2 и 3, соответствующими треугольным координатам.

При задании функции перемещений в треугольном элементе для узловых перемещений принимается та же нумерация, что и для соответствующих узлов, т. е. pqr. В соответствии с установившейся традицией разыскиваем функции перемещений для элемента в

A,(/i)=li(-) Для/>1

= 1 для 1 = 0

(8.11)

при i=p, q или г соответственно.

В качестве примера рассмотрим построение функции формы /V200. Имеем т=р=2, q=r=0, поэтому N =No(L2) = l, = = /V (L3)=l и

Л2 (/i) = Xi?ii±il = L,(2L, 1).

Следовательно, yV2oo=Li(2Li-1). Непосредственно устанавливается, что yVo20=L2(2L2-1), Л002=8(2£з-1), A011 = 4L2L3, yViio =

=4LiL2 и yVioi=4L3Li. Имеются случаи, когда желательно оперировать с обобщенными, а не с узловыми степенями свободы. При этом полезно знать, что полный полином степени т можно записать в треугольных координатах в виде

А = S aiLPLlLa (p + q + rm), (8.1а)

где в сумму входят все однородные члены степени т, т. е. показатели функций (}юрмы в точности определяются трехцифровыми ин-

виде

1/2 (т+1) (m + 2)

A=LNJ{A}= 2 Ля.г,г. (8.25)

Так, при т=1 функция перемещений дается формулой

A=yV,o Aio +/VoioAoio+/VooiAooi, (8.25а)

а для т=2, согласно рис. 8.14(a),

A=yV2ooA2oo+AiioAiio+. . .+Aioiioi (8.25b)

и т. д. для полинома любого порядка.

Теперь необходимо задать способ построения функций (}юрмы Np так, чтобы они удовлетворяли обычным условиям, накладываемым на данные функции (например, N = 1 в точке pqr; Npg=0 во всех остальных точках). Как показано в одномерном случае, этим условиям можно удовлетворить, задавая функции формы в виде произведений функций соответствующих координат и проводя лагранжеву интерполяцию в каждом из направлений. По аналогии с одномерным случаем для применяемой функции имеем

yVp (Lb и Ls)=N,{L,)N(L2)NAL ), (8.12а)

где члены в правой части соотношения задаются в виде

3{L L,) = iLiy(L,ydA.

Так как это выражение представляет собой частный вид (8.26) при d=0, b=e, c=f, то

3{1г, La) = 2А (4Д2)- (-26)

Имея в виду приведенные выше рассуждения, интересно отметить некоторые не столь заметные преимущества представлений в треугольных координатах. Во-первых, задание узлов в представ-

дексами узлов согласно рис. 8.14(a) и (Ь). Для кубического разложения, например, имеем

А = {LiY а, + (L,f а, + {Lf а, -f (L,) L,a, + {L.f L,a, +

Располагая выражением выписанного типа при построении опорной матрицы жесткости, можно использовать преимущества явных формул интегрирования для треугольного элемента.

Второй часто выполняемой при представлении полей в треугольных координатах операцией, особенно при рассмотрении соотношений между деформациями и перемещениями, является операция дифференцирования. Например, рассмотрим деформацию ej.= =ди/дх. Если рассматривается квадратичное поле перемещений, где и выражается в виде Л2оо 2оо+. . .+Aioi ioi, то первый член в выражении для равен

дх дх дх

Замечая, что, согласно определению Lj (8,22), dLildx=biJ2A (i= = 1,2, 3), поэтому

T = &(4L,-1).

И наконец, что наиболее важно, можно выписать простое явное выражение для интегралов, которое является также обобщением формул одномерного случая. Искомые интегралы имеют вид

2Ab\ cl dl

-(b+c+d+2)r (-26)

(Cp. с (8.13).) Из (8.20) вытекает, что только две координаты независимы и интеграл всегда можно преобразовать к виду