изучаются матрицы преобразования, при этом рассмотрение несколько выходит за рамки обычного применения преобразований при замене систем координат. Это позволит определить операции по уменьшению числа параметров в получаемых решениях. В заключение описываются операции, выполняемые с матрицей жесткости элемента для выделения форм движения как твердого целого.

2.1. Система координат

Ниже наиболее часто будет использоваться ортогональная система координат, оси которой, изображенные на рис. 2.1, обозначены символами X, у и г.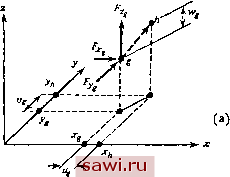

Рис. 2.1. Обозначения дая сил и перемещений (а) Перемещение из точки g в точку Л; (Ь) силы, моменты и соответствующие им перемещения.

Действие нагрузок на упругую конструкцию вызывает перемещение точек тела, включая смещение точек относительно друг друга. В настоящей главе рассматривается поведение элементов конструкций в целом, определяемое смещением точек тела под

dv Эг

С. =

действием приложенных к этим точкам систем нагрузок. Детальное изучение относительных смещений точек внутри тела (деформаций) и распределения усилий, отнесенных к единице площади, для внутренних точек (напряжений) будет проведено в последующих главах, особенно в гл. 4-6, где рассматриваются такие факторы, как распределенные нагрузки и начальные деформации, обусловленные тепловым расширением.

Совокупность осей координат для конструкции в недеформи-рованном состоянии вводится согласно рис. 2.1. Эти оси остаются неподвижными в процессе деформации конструкции, и смещения точек тела определяются относительно указанных осей. Рассмотрим для свободного от нагрузок недеформированного тела малый элемент объема с центром в точке g (см. рис. 2.1 (а)). На этот элемент действует вектор усилий с компонентами Fg, Fyg, Fg. Под действием этой силы малый элемент объема сместится в точку, обозначенную на рис. 2.1 символом h. Трансляционное смещение элемента задается в виде Ug=Xh-Xg, Vg=y-yg, Wg=Zii-z. Согласно обозначениям для компонент вектора сил, указанные величины изображаются так же, как компоненты вектора, отнесенного к соответствующей точке недеформированного тела. Положительные значения сил и компонент смещений отвечают положительному направлению осей координат.

В книге, за исключением последней главы, описание поведения гела ограничено линейным случаем. Применительно к рассмотренным выше силам и трансляционным смещениям это означает, что компоненты вектора силы остаются неизменными при перемещении элементарного объема из в Л. Кроме того, такая механическая характеристика, как работа, производимая силами Fg, Fyg, Fна перемещениях Ug, Vg, Wg, не зависит от вида пути в точку Л.

Задание трансляционных смещений само по себе недостаточно для полного описания смещений конструкции. В задачах, где рассматриваются балки и конструкции рам, тонкие пластины и оболочки, исследователь, как правило, делает упрощающее предположение, согласно которому отрезок, проведенный перпендикулярно нейтральной линии (для балок и рам) или срединной поверхности (для пластин и оболочек) в недеформированном состоянии, остается нормальным к нейтральной линии или срединной поверхности и после деформации. Мерой смещения точек указанных конструкций служит угол 6 поворота нормали, отмеряемый от недеформированного состояния. Часто предполагается, что значение этого угла равно тангенсу угла наклона нейтральной линии или срединной поверхности. Если ввести систему координат, изображенную на рис. 2.1 (Ь), то угловые смещения точки k призматического элемента, расположенного вдоль оси х, определяются величинами

(Здесь для простоты исключены из рассмотрения силы, задающие трансляционное смещение в точке /.) Заметим, что положительные углы определяются согласно правилу правой руки: если расположить правую руку так, чтобы большой палец указывал на положительное направление оси, то остальные пальцы охватывают ось в положительном направлении вращения. В соответствии с этим правилом Qy имеет отрицательный знак, так как вращение в положительном направлении приводит к отрицательным смещениям w. Силовыми величинами, соответствующими угловым смещениям, являются векторы моментов с компонентами М Myj и Mj.

Следует отметить, что производные от перемещений можно рассматривать как характеристики поведения конструкции в заданных точках, не приписывая физический смысл этим производным. Действительно, при расчетах методом конечных элементов могут быть использованы и используются производные от перемещений второго и более высокого порядков (например, dwldx, dwldx). Физическая интерпретация этих величин часто не очень наглядна. Это же относится и к отвечающим им силовым величинам. Однако указанные трудности окупаются повышением эффективности при расчетах.

Как уже указывалось, описание поведения детали конструкции в целом - в нашем случае описание поведения отдельного конечного элемента - осуществляется с помощью компонент сил и смещений, заданных в определенных точках тела. Такие точки обычно называются узловыми точками. Они также называются точками соединения, потому что в большинстве случаев применения метода конечных элементов они соответствуют действительным точкам соединения элементов, образующих полную, или глобальную, аналитическую модель конструкции в целом. Существует много случаев, когда эти точки не имеют столь очевидного физического смысла. Тем не менее в книге понятия узловая точка и точка соединения не будут различаться.

Рассмотрения этой главы требуют краткой и четкой формы записи сил и перемещений в узловых точках заданного элемента конструкции. Силам и перемещениям соответствуют вектор-столбцы {Г-} и {Л}. (Скобки { } означают вектор-столбец.) Для изображенного на рис. 2.1 (Ь) элемента, на который действуют силы в точке g и моменты в точке / , имеем

{F} =