8.6. Тетраэдральные элементы

Изображенный на рис. 8.15 тетраэдр есть трехмерный аналог плоского треугольного элемента. Подобно случаю плоского треугольного элемента определение функций формы и интегрирование энергии деформации осуществляются здесь в тетраэдральных координатах, которые являются аналогом треугольных координат из разд. 8.5.

Cvol),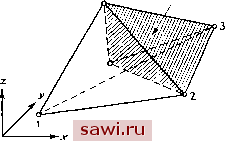

Рис. 8.15. Базисный тетраэдр.

Местоположение точки внутри тетраэдра, полный объем которого обозначен через (vol), можно определить при помощи следующего набора отношений:

г . (vo)i f (vq)2 f (Уо1)з , (vol)4 /о

(vol) (vol) (vol) (vol)

где (vol)i (i=l, . . ., 4) обозначает объем, заключенный между линиями, соединяющими точку с вершинами тетраэдра, противолежащими вершине i. На рис. 8.15 изображен (vol)i. Величины Li, . . ., Li представляют собой тетраэдральные координаты. С учетом (8.27) имеем

Li-fL,-fL3-fL4=l (8.28)

лении элементов высокого порядка (см. рис. 8.14) автоматически указывает место расположения узлов. Заметим далее, что изображенные на этих рисунках массивы в точности соответствуют различным уровням в треугольнике Паскаля. Поэтому каждому порядку интерполяции в треугольных координатах отвечает полное полиномиальное представление соответствующего порядка. Ранее отмечалось значение понятия полноты и, по-видимому, по этой причине треугольные элементы занимают особое место в конечно-элементном анализе. Другая причина их распространенности состоит в возможности гибкого их использования при представлении геометрических объектов сложной формы.

и, дополняя это уравнение соотношениями между декартовыми координатами точки X, у, г м тетраэдральными координатами, получим

1 1 1 Г

Xs Х Уг у. Уз Уа

Обрашая матрицу, заключаем, что

L =-1- 6 (vol)

где (VOL);- объем, заключенный между стороной тетраэдра 1 и лучами, проходящими через ее вершины и начало координат; (vol) равен одной шестой значения детерминанта выписанной выше (4х4)-матрицы, а d., С. и Сз.- детерминанты возникающих при обращении (ЗхЗ)-подматриц.

Имеющаяся аналогия между тетраэдральными и треугольными координатами позволяет применить изображенный на рис. 8.16 тетраэдр Паскаля при определении совокупности членов разло-

[(V0L), + Qx + Qi/ + C3z] Ц=\.....4), (8.29)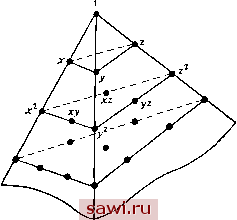

Рис. 8.16. Обобщение на трехмерный случай треугольника Паскаля.

жения для полных полиномов любого порядка, задаваемых в узловых точках элемента, а также функций формы, соответствующих указанным полиномам. Типичная тетраэдральная функция формы помечается четырьмя нижними индексами в виде jVp , и следующим образом зависит от Lj, . . ., Lt.

Np, {Lu L 1з, U) = Np(U) NiU) NAL3) NsiU), (8.30)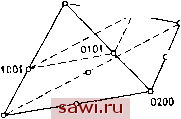

1100 2000

Рис. 8.17. Нумерация узлов для тетраэдрального элемента о квадратичным полиномиальным представлением.

тичных функций на рис. 8.17. Заметим, что сумма четырех индексов должна равняться т=2 в этом случае и порядку т. выбранной функции в общем случае. Соответствующая формула для Ni, i=p, q или г дается опять выражением (8.11).

При интегрировании в объемных координатах будем иметь следующую формулу для типичного интеграла:

5(L L L3, L,)= S {L,Y{L,){L,Y{L,Yd{vo\)=

6 (vol) a! b\ cl d\

(a + ft+c+d + 3)l-

(8.31)

Вследствие (8.28) только три из координат независимы, и поэтому можно упростить выписанное выражение. Предположим, что исключение (Li)** приводит к следующему преобразованию интеграла Ц ):

5(L,. L L,)=\ {L,Y(Ly(L,)id{vol),

тогда имеем

(t.. L.. ,8.3,a,

Подробное исследование тетраэдральных координат приводится в [8.9].

т. е. представляется в виде произведения функций от соответствующих объемных координат. Введение соответствующих нижних индексов аналогично случаю треугольных координат и иллюстрируется для тетраэдрального элемента, построенного на базе квадра-

0002

--0011

>0020 (0110