Во внутренних точках элемента силы {F} будут известными величинами, полученными в результате рассмотрения энергетически эквивалентных нагрузок, приложенных сосредоточенных нагрузок и т. д., либо эти силы равны нулю, так как указанные точки не соприкасаются с другими элементами конструкции. Следовательно, исключение внутренних мод проводится в точности по схеме конденсации из разд. 2.8.

Здесь уместно отметить, что внутренние моды более точно назвать как дутые моды , т. е. моды, имеющие отличные от нуля амплитуды внутри элемента и обращающиеся в нуль на его сторонах. Это происходит в силу того, что амплитуда функции формы равна единице для рассматриваемой степени свободы и нулю для остальных степеней свободы.

Второй способ исключения нежелательных степеней свободы состоит в непосредственной модификации функции формы таким образом, чтобы она выражала только требуемое число параметров. По видимому, простейшей схемой исключения степеней свободы из

8.7. Внутренние моды и редукция к простым формам

Ранее отмечалось, что желательно выписывать уравнения элемента, отвечающие узлам, расположенным лишь в вершинах и на сторонах элемента. С внутренними степенями свободы трудно оперировать. Также было показано, что внутренние степени свободы естественным образом вводятся при построении функций формы для элементов высокого порядка. Аналогичная ситуация возникает, если соотношения выводятся на основе обобщенных координат, причем число указанных координат превышает число степеней свободы, отвечающих сторонам и вершинам элемента. Эти дополнительные обобщенные координаты можно рассматривать как внутренние степени свободы. В этом разделе излагается два способа, с помощью которых можно исключить внутренние степени свободы. Кроме того, изучается вспомогательная задача построения функций формы для элементов с различным числом узлов на соответствующих сторонах элемента.

Рассмотрим сначала случай, когда внутренние степени свободы естественно возникают при построении функций формы для элемента высокого порядка. В этом случае матрица жесткости элемента может быть построена с использованием всех степеней, представленных в функции формы. Предположим, что внутренние степени свободы обозначены нижним индексом Ь, а степени свободы, отвечающие сторонам и вершинам элемента,- нижним индексом с. Тогда построенная матрица жесткости может быть записана в виде

J]. (8.32)

рассматриваемых выражений является введение соотношений, свя-зываюших исключаемые степени свободы с оставшимися степенями. Рассмотрим, например, изображенный на рис. 8.14(a) треугольный элемент, построенный при помоши квадратичного поля перемещений, функция формы для которого подробно изучалась в разд. 8.5. v Предположим, что необходимо исключить узел ПО. Можно потре-эть, чтобы перемещение вдоль данной стороны было линейно; тогдаАпо=(А2оо+Ао2о)/2, и, подставляя в полное выражение для поля перемещений, получим

N§ 0200+ N20020+ N ооЛоо2+ МопАоп + МюЛюи

где ЛУ2оО=(ЛУ200+/2ЛУ11о), Л20 = (ЛУ020+/2ЛУ110).

Предложенный подход может быть успешно применен и для прямоугольных областей. Например, выше была указана необходимость исключения внутреннего узла изображенного на рис. 8.7(b) прямоугольного элемента с биквадратным полем перемещений. Перемещение в этой точке можно задать в виде среднего значения от перемещений на серединах сторон: A5=V4(A2+A4-(-Aj+Ag). Можно ~ . также включить при усреднении и узлы в вершинах прямоуголь ника с помощью взвешенного учета соответствующих степеней свободы. Таким образом, можно выписать набор различных выра-жений в терминах заданной сокращенной системы степеней свободы.

Более элегантный подход [8.10] к построению специальных функ- I , ций перемещений можно осуществить с помощью процедуры, включающей суперпозицию отдельных функций перемещений. Прежде чем приступить к реализации данного подхода, который здесь будет использован только для прямоугольных элементов, удобно выразить функции формы в терминах безразмерных координат (i, т]) с началом в центре прямоугольника. В этой связи функции формы для прямоугольников задаются в физической системе координат (х, у), начало которой расположено в вершине прямоугольника.

Чтобы осуществить это преобразование (см. рис. 8.18(a)), используем соотношения =(х-xJAx-и y] = (y-y)/(y-yi), где Х5 и у-координаты центра прямоугольника, а Xi и г/i- координаты нижней левой вершины. Тогда безразмерные координаты i: четырех угловых точек всегда равны +1 илн -1.

. Рассмотрим теперь построение функции формы для прямоуголь-

ного элемента с биквадратным полем перемещений, в котором необходимо исключить внутреннюю точку (см. рис. 8.18(a)). Функцию формы для лежащего на стороне элемента узла 2 можно получить в виде произведения квадратичной функции (1-), соответствующей направлению вдоль рассматриваемой стороны, и линейной функ-ции 1/2(1-Ц) для перпендикулярного направления. Поэтому полная функция формы для этой точки равна N-Uil-) (1-in). Построение функции формы для угловой точки приводит к более сложной задаче. Во-первых, как показано на рис. 8.18(b) для точки

1, билинейная функция дает ненулевые смещения в точках 2 и 4. Задать нулевые смещения в этих точках можно, вычитая из данной функции 1/2функции формы (см. рис. 8.18(c)) и 1/2функции формы Л4. [Согласно предыдущим рассуждениям, Л4=2(1-I) (1-п ).]. Следовательно,

Ai=V4(l-?) (1-л)-4(1-?) (1-г1) - V4(l-E) (1-т1).

Можно показать, что полиномиальные коэффициенты, входящие в рассмотренные функции, лежат в отмеченных на рис. 8.18(c) областях, т. е. они отвечают квадратичным функциям, соответству-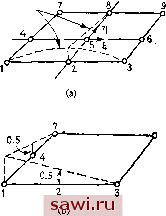

Рис. 8.18. Непосредственное построение поля перемещений для восьмиузлового прямоугольного элемента.

ющим разложениям вдоль сторон, умноженным на линейные функции в перпендикулярном направлении. С помощью изложенной методики схема легко распространяется на построение выражений любого порядка вдоль сторон элемента для двух- и трехмерного случаев.

9 № 2647