8.8. Изопараметрическое представление [8.11]

Изопараметрические элементы - это элементы, в которых функции, используемые для представления поведения при деформировании, используются также и для описания геометрических характеристик элемента. Построение изопараметрического элемента представляет собой преобразование безразмерного прямоугольного элемента с заданным числом узлов в реальный криволинейный элемент с тем же числом узлов. Так, если функции, задающие поле перемещений в формулировке, основанной на принципе минимума потен-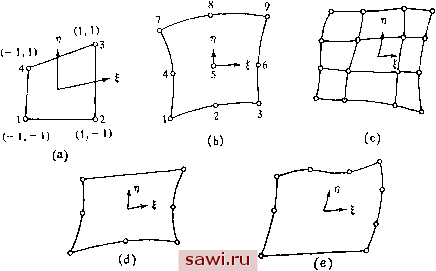

Рис. 8.19. Изопараметрические элементы.

циальной энергии, суть кубические полиномы, стороны элемента описываются теми же кубическими функциями. Если межэлементно совместные поля перемещений выбираются для описания геометрических характеристик элемента, то в объединенной аналитической модели деформированный элемент состыковывается с любым подобным ему соседним элементом без разрывов геометрических характеристик.

В двумерном анализе простейшим четырехсторонним изопараметрическим элементом является изображенный на рис. 8.19(a) элемент, в котором для обобщения прямоугольника на случай произвольного четырехугольника используется линейное поле. Лучшее задание криволинейных сторон достигается для элементов более высокого порядка, например изображенных на рис. 8.19(b) и (с).

8.8. Изопараметрическое представление [8.11] 259

где квадратичные и кубические функции, используемые для представления перемещений, применяются также для задания границ. Представляют, кроме того, практический интерес изображенные на рис. 8.19(d) и (е) элементы смешанного типа с различным числом узлов на каждой стороне и при наличии или отсутствии внутренних узлов.

Несущественно, что те же самые функциональные представления для перемещений используются и для задания геометрических характеристик элемента. Если порядок функций, представляющих геометрические характеристики, ниже порядка функциональных представлений для перемещений, то рассматриваемые элементы называются субпараметрическими; если же порядок функций, задающих геометрию, выше, то элементы называются суперпараметрическими. Изопараметрические, суб- и суперпараметрические конечно-элементные представления являются, пожалуй, наиболее важными при анализе трехмерных упругих тел Соответствующие вопросы рассматриваются в гл. 10. Трехмерный анализ обычно требует чрезвычайно большой памяти ЭВМ. Если конструкция имеет криволинейную поверхность, то при регулярном конечно-элементном представлении обычно требуется большое число элементов для воспроизведения геометрических характеристик конструкции без существенного улучшения в представлениях полей напряжений или перемещений. Поэтому представление с помощью изопараметри-ческих элементов уменьшает затраты на описание геометрии.

Для описания операций, выполняемых при построении изопара-метрических элементов, достаточно рассмотреть двумерный случай. На первом шаге требуется задать систему безразмерных координат (I, т]) с началом в центре элемепга Jin операции рассмотрены в разд. 8.7 для плоского прямоугольного элемента. Заметим еще раз, что для любого прямоугольника =(а;-х)1{х-х) и 1 = (У-f/c)/(f/c-f/i). где Хо и t/o- координаты центра прямоугольника, а Xi и t/i- координаты нижней левой угловой точки. Вспомним также, что безразмерные координаты четырех угловых точек всегда равны +1 или -1 (см. рис. 8.19(a)).

На втором шаге необходимо выразить функции формы L N J = =-\ Ni . . . Ni . . . Nn \ в терминах безразмерных координат. При билинейной интерполяции, например, имеем (для узлов, определенных на рис. 8.19(a))

LN J=V4L(l-l)(l-il) (1+1)(1-Л) (1 + )(1+г1) (l-)(l+ri)J.

Определим функции формы, которые в силу сказанного записываются в виде N (I, fl) J , и зададим координаты хиу элемента в виде

*=LN(l,ri)J{x}, f/=LN(l,ri)J{y}, (8.33)

где {х} И {у} включают координаты х я у узловых точек элемента,

{х}= LX,. . .Xi. ..XnJ\ {у}= LУг. . -yi- ..УпГ. (8.34) Таким образом, x=Xi, у=У1 в точке i. Соответственно имеем

=LN(Lil)J{u}, t=LN(E, n)J{v}, (8.35)

где (u }= L Ul 2 из Ui J (v }= iviVVaVtJ.

Чтобы построить матрицу жесткости элемента, необходимо найти деформации, которые в свою очередь являются производными по X и 1/ от перемещений. Однако теперь перемещения являются функциями от координат I и ц. Следовательно, необходимо найти связь между производными по X иуи производными по и т1.Это можно осуществить, применяя правило дифференцирования сложных функций. Получим

dN; дх dNi , ду dNi

dl - dl dx dl dy dNj ddNj dy dNi dl] дт] dx Sri dy

(8.36)

Используя (8.33), определим dx/dl= \ dfi/dlj {x} и аналогичным образом дх/дх] и т. д. Поэтому (8.36) можно записать в виде

dNi \ i dNi

dNj 1 dNi

. дц) \ dy I

[J]2X2 =

(8.37)

(8.38)

Как принято в матричной алгебре, матрица первых производных, т. е. (2х2)-матрица IJ], называется матрицей Якоби.

Для иллюстративного случая билинейного элемента (см. рис. 8.19(a)) имеем

-]=1-(1-л) (1-л) (1 + л) -(H-л)J, J=L-(i-E)-(i-i)(i + i) (i + i)j.

Поэтому верхний левый эле.мент в [J] равен

п=/4[(1-л) (;2-;1)+(1+л) (xs-x,)]. Аналогично находятся выражения для У12, J 21 а У аз.