где так же, как и в (6.72а),

j[N ]T[E]-[N ]/rfЛ

(9.9)

Здесь не приводятся основные соотношения для формулировки смешанных вариационных принципов в случае плоского напряженного состояния; в этой главе лишь кратко излагается роль этих принципов при формулировке элементов. В работе [9.11 .можно найти подробное изложение вопросов, связанных с функционалом Рейсснера, в случае плоского напряженного состояния.

9.2. Треугольные плоско-напряженные элементы

9.2.1. Элементы, построенные на базе предполагаемых перемещений

В этом разделе рассматриваются плоско-напряженные треугольные элементы, построенные в предположении, что поля перемещений представлены соответственно полными линейными, квадратичными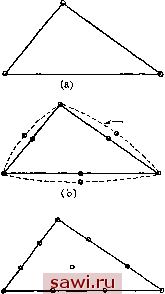

д.х ду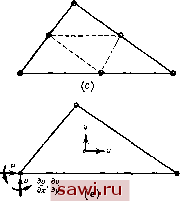

Рис. У.2. Возможные виды треугольных элементов; (а) треугольный с постоянным значением деформации (CST-элемент); (Ь) треугольный с линейной деформацией (LST-элемент); (с) образованный из четырех треугольников с узлами на серединах сторон; (d) десятиузловой треугольный с квадратичной деформацией (QST-элемент); (е) треугольный с квадратичной деформацией, включающий производные в качестве степеней свободы.

dNaoo 5/Vo5o dNoo2 dNuo dNpU dNipi dx dx dx dx dx dx

(9.11)

и аналогично для других векторов из (9.6). Первый член в (9.11) равен, как показано в разд. 8.5,

= (41,-1). (9.12)

Все остальные члены получаются также легко в результате дифференцирования.

И кубическими полиномами. В разд. 8.5 показано, что теоретически для треугольных элементов нет ограничений на степень полиномиального представления, так как легко расположить узловые точки внутри и на границе элемента, чтобы учесть функцию любого порядка. Однако на практике ценность элементов, основанных на полиномах, степень которых превышает третью, является дискуссионной. В этом случае, с одной стороны, существенно труднее выписать коэффициенты для элемента, а с другой - необходимость измельчения конечно-элементной сетки, моделирующей конфигурацию реальной конструкции, делает недействительными преимущества более усложненных представлений поведения элемента.

На рис. 9.2 изображены элементы, обсуледаемые в этом разделе. Основной элемент (см. рис. 9.2(a)) со степенями свободы в вершинах треугольника построен в предположении постоянства деформаций, что равнозначно постоянству напряжений или линейности перемещений. Этот элемент часто называется CST-элементом. Матрица жесткости этого элемента для изотропного материала получена с помощью альтернативных процедур в разд. 5.2 и 6.4 и представлена на рис. 5.4. Так как этот вывод в разд. 5.2 проведен детально, здесь не требуется дополнительных пояснений.

По мере усложнения следующим элементом является изображенный на рис. 9.2(b) шестиузловой треугольный элемент, построение которого основано на задании полных квадратичных полиномов для перемещений и и v. Так же как в разд. 8.5, имеем

=A200 200 + A020 OSO+A/ a o02+A/iio 110 + A/ou oil + A/loi 10i (8.25b)

и аналогичное выражение для v. В терминах треугольных координат из (8.Па) и (8.12а) получим

A2 o = ii(2Li-l), / 20 = 2 (22-1). N 2=L,(2L3-l), (9Л0) Лио = 4112, A n = 4L2L3, NiiiLLi.

В этом случае после применения соотношений между деформациями и перемещениями (4.7) приходим к (9.6), где {и}=1 2оо. . ю! J,

Матрица жесткости формулируется с использованием (9.7). На практике интегрирование тройного произведения [DjfE] [D] по области, занимаемой элементом, выполняется численно в виду сложности явных выражений для коэффициентов жесткости элемента. Однако получение явных выражений возможно, если построение ведется в терминах коэффициентов жесткости для CST-элементов [9.2]. Явные выражения для коэффициентов матрицы жесткости элементов более высокого порядка оказываются громоздкими.

Квадратичное поле перемещений приводит к линейным распределениям деформаций (или напряжений) в треугольном элементе, такой элемент обычно называется LST-элементом. Может показаться, что объединение четырех CST-элементов, как показано на рис. 9.2(c), приведет к тому же результату, что и один LST-элемент. Однако LST-9jieMeHT определяет непрерывное (линейное) напряженное состояние внутри элемента, а совокупность CST-элементов дает четыре различных постоянных значения каждой компоненты напряжения.

Внутри LST-элемента дифференциальные уравнения не удовлетворяются. Этот факт был продемонстрирован ранее в разд. 4.5 с помощью полиномиального представления полей перемещений U, и и, а не с помощью рассмотрения функции формы. Очевидно, условия равновесия в узлах, находящихся внутри всех элементов более высокого порядка, также нарушаются.

Как показано на рис. 9.2(b) штриховыми линиями, LST-элемент подходит для представления в изопараметрической форме. Операции, реализующие это представление, были описаны в разд. 8.8. Вообще говоря, все обсуждаемые здесь и в последующих главах конкретные элементы подходят для представления в изопараметрической форме. Так как детали построения во всех случаях соответствуют изложенным в разд. 8.5, то далее, за исключением частных случаев, не будут обсуждаться вопросы, связанные с изопараметрической формой представления.

Для дальнейшего улучшения представления может использоваться треугольный элемент, базирующийся на полных кубических (десятичленных) полиномах перемещений для компонент и я v. В этом случае встречаются два альтернативных способа расположения степеней свободы. В первом - изображенном на рис. S.2(d)- задается обычным образом набор из 10 узловых точек, и в качестве степеней свободы выбираются значения и я v в каждом узле. Во втором - изображенном на рис. 9.2(e) - узлы задаются лишь в вершинах, где наряду с и и у задаются также и производные от этих величин {du/dx=Ux и т. д.). Это приводит к появлению 9 степеней свободы соответственно для каждой компоненты и я v, т. е. всего к 18 степеням свободы. В полном разложении обеих величин и я V имеется 20 степеней свободы. Дополнительные две степени сво-