боды можно задать в виде двух компонент смещения центральной точки элемента. Можно исключить эти две степени свободы с помощью процедуры конденсации, описанной в разд. 2.8 или с помощью более элегантных процедур, описанных подробно в работах [9.4-9.6].

Кроме того, можно разделить исходный треугольный элемент на три треугольника, выбрать внутри каждого из них девяти-или десятичленные полиномы для и и v и исключить внутренние степени свободы, налагая условия непрерывности перемещений. Этот подход более распространен для изгибаемых треугольных элементов и обсуждается в связи с этим в п. 12.3.2.

Элементы более высокого порядка с наборами узлов, соответствующих треугольнику Паскаля, т. е. с узлами вдоль сторон и внутри элементов, приводят к более общим уравнениям жесткости с большей шириной ленты в соответствующих ленточных матрицах по сравнению с элементами, степени свободы которых сосредоточены лишь в вершинах. Причину этого можно выяснить, добавив совокупность из двух треугольных элементов к конечно-элементной

9 Эополнительных узлов- по 1 степени свободы на узел

о 1 степени свободы на узе/г 6 степеней свободы на узел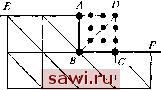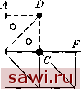

Рис. 9.3. Сравнение альтернативных форм задания степеней свободы, (а) Объединение двух треугольных элементов с квадратичной деформацией; (Ь) производные в качестве узловых степеней свободы.

модели с границей, задаваемой на рис. 9.3 точками Е, А, В, С, F. Если, как показано на рис. 9.3(a), добавим элементы с представлением деформаций в них в виде квадратичной функции, которые и.ме-ют 10 узлов (тип элемента совпадает с изображенным на рис. 9.2(d)), то в соответствующей ленточной матрице возникают дополнительные коэффициенты, отвечающие 18 степеням свободы. Добавление двух элементов с квадратичным распределением деформаций внутри них и со степенями свободы в виде производных в узлах и в центре треугольников (тип элемента показан на рис. 9.2(e)) приводит, однако, к появлению дополнительных 10 степеней свободы. Различие объясняется тем, что в точке D в элементах со степенями свободы в виде производных степени свободы взаимосвязаны.

Увеличение ширины ленты в ленточной матрице приводит к возрастанию стоимости решения уравнений при проведении расчетов. Другое преимущество элементов со степенями свободы в виде производных заключается в том, что производные, используемые как степени свободы, непосредственно пропорциональны деформациям и, следовательно, напряжениям, так что граничные условия в напряжениях могут быть заданы непосредственно. Недостатком является то обстоятельство, что для плоского напряженного состояния силовые характеристики в узлах, отвечающие степеням свободы в виде производных от перемещений, не наделены ясным физическим смыслом.

9.2.2. Вопросы аыбора треугольной сетки

Треугольный элемент завоевал популярность благодаря простоте задания постоянного значения деформации внутри элемента, а также в виду удобства описания геометрических характеристик сложных конструкций. В то же время для сложных конструкций возникают определенные трудности при выборе подходящей сетки разбиения из имеющегося разнообразия вариантов.

В связи с выбором набора треугольных элементов следует прежде всего отметить отсутствие геометрической изотропии . Чтобы проиллюстрировать это утверждение, рассмотрим задачу анализа напряженного и деформированного состояния бруса, изображенного на рис. 9.4. Наборы элементов, представленные соответственно на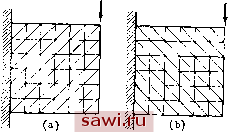

Рис. 9.4. Возможные варианты разбиения для рассматриваемой задачи.

рис. 9.4(a) и (Ь), хотя и содержат равное количество элементов одинаковой формы, приводят к различным численным решениям для перемещений и напряженнй. Эти различия могут быть малы для густых сеток разбиения, используемых при практических расчетах, однако было бы желательно использовать все и.меющиеся возможности, приводящие к исключению или уменьшению этих расхождений. Для настоящего случая изображенная иа рис. 9.4(c) схема с очевидностью решает проблему. Однако для многчх реальных кон-

струкций получить решение не так просто и при расчетах следует учитывать некоторое несовершенство указанных разбиений.

Как видно из предыдущего примера, геометрическую изотропию можно сохранить, если конструкция имеет прямоугольные очертания или содержит лшого пря.моугольных областей. Преобладание на практике конструкций прямоугольного очертания приводит к использованию элементов-кирпичиков , когда проектировщик применяет прямоугольные элементы, состоящие в действительности из нескольких треугольных элементов. На рис. 9.5 изображены два таких элемента, в каждом из которых сохраняется геометрическая изотропия.

(а) (Ь)

Рис. 9.5. Способы объединения треугольников при построении прямоугольника.

Изображенный на рис. 9.5(a) прямоугольный элемент построен из четырех треугольных. Два треугольника, у которых толщина в два раза меньше толщины реальной пластины, соприкасаются вдоль диагонали, соединяющей точки 1 и 3. На них лежит пара треугольников той же толщины, соприкасающихся вдоль диагонали, соединяющей точки 2 и 4. Можно также рассмотреть четыре треугольника, расположенных так, как показано на рис. 9.5(b), с центральной точкой 5, которая исключается из результирующей матрицы жесткости для прямоугольного элемента с помощью процесса конденсации, описанного в разд. 2.8.

Одним из неудобств рассмотренных выше схем является трудность интерпретации вычисленных напряжений подходящим для процесса проектирования образом. При проектировании прямоугольных панелей требуется задание постоянных или линейных полей напряжений в элементе. Однако при реализации схемы согласно рис. 9.5(b) поле напряжений внутри прямоугольника описывается четырьмя различными значениями каждой колшоненты напряжений. Обычно для всего прямоугольника эти значения усредняют. Проблема заключается в том, что четыре дискретных значения могут различаться существенно, вызывая сомнение в точности полученных средних величии.

Теоретические исследования [9.7] скорости сходимости численных решений к точным решениям определяющих дифференциаль-