щему виду уравнений жесткости для элемента (исключая другие типы специальных сил):

{F}=[k]{A}-{F*}. (6.16а)

(6.121)

{F=j[K]T.TdS.

Тогда при указанных условиях не изменяется вид закона, связывающего напряжения и деформации о=[Е]е, и соотношение e=[D] (А) также не меняется, поэтому выражение o=[S] (Л) можно использовать при подсчете напряжений, вызванных распределенными нагрузками.

Рассмотрим изложенные вопросы для изображенного на рис. 9.8(a) стержневого элемента, нагруженного равномерно распределенной нагрузкой интенсивности д. Конструкция разбива-

А,Е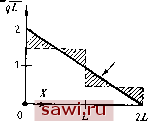

Вычислено из

Точное решение

2-1 2

Рис. 9.8. Подсчет напряжений в равномерно нагруженных стержневых элементах конструкции, (а) Рассматриваемый элемент конструкции; (Ь) аналитическое представление; (с) распределение напряжений; (d) отдельные элементы.

ется на два элемента согласно рис. 9.8(b). Для каждого элемента задается энергетически эквивалентная нагрузка {?\=qLI2\ 1 1 J . Уравнение жесткости для всей конструкции имеет вид

\qm\ L

2 -1 -1 1

решая которое получим

1 -1 -1 1

поэтому F2-3=-qL [знак минус соответствует растяжению, см. 9.8(d)l, а з 2=0. Аналогично для элемента 1-2 находим, что Fi y=qL и /i a=-2 qL (снова знак минус означает растяжение на левом конце). Разделив эти силы на площадь поперечного сечения Л, получим точное распределение напряжений *>, изображенное на рис. 9.8(c). Таким образом, правильные напряжения получаются, если вначале находятся силы в узлах, которые затем преобразуются в напряжения. Выражения для узловых сил могут включать не только распределенные нагрузки, но также силы инерции [т] {Л}, как в (6.16), или другие виды распределенных воздействий.

Заметим, что узловые силы локально (в узлах) преобразовываются в напряжения. Для стержневого элемента, когда существует взаимно однозначное соответствие между компонентами сил в узлах и искомыми компонентами напряжений, это - непосредственно выполняемая операция. Однако для плоского напряженного состояния существуют три компоненты напряжений и только две компоненты силы в каждом узле. Указанное рассогласование присуще большинству многомерных напряженных состояний. Поэтому при подсчете напряжений обычно пренебрегают поправкой , вносимой членом {F}, и вновь используют формулу o=[S] {А}. Возникающая при этом ошибка отражена на рис. 9.8(c) заштрихованными областями, откуда видно, что величина ошибки становится малой, если использовать, как это часто бывает на практике, большое число элементов.

* Интересно отметить, что точные значения напряжений получаются в узлах соединений для любых распределений прикладываемых нагрузок, если применяются энергетически эквивалентные силы, вычисленные на основе функций формы, которые представляют точное решение соответствующих однородных (с нулевыми силами) определяющих дифференциальных уравнений. Это происходит потому, что все соответствующие условия (равновесия, совместности) в этих точках при энергетически эквивалентных нагрузках выполняются точно (см. [9.11]).

так ЧТО 2=2 (дЬУАЕ), из=2дЬЧАЕ. Матрица жесткости для стержневого элемента представляет собой матрицу-строку (£/L) -1 1 J , и можно предположить, что в каждом элементе напряжение постоянно, т. е. а1 2=УдЬ/А, a =qLIA. На рис. 9.8(c) данное напряженное состояние изображено штриховыми линиями. Точное распределение, полученное в результате решения задачи, показано сплошной линией.

Чтобы предложить совершенно иной подход к расчету напряжений, рассмотрим основные уравнения, связывающие силы и перемещения для элемента. Для элемента 2-3 имеем

Процедура, основанная на начальном вычислении узловых сил, позволяет соответствующим образом интерпретировать процедуру, базирующуюся на использовании матрицы жесткости. В формуле (6.16а) (что и учитывалось выше) член [к] {А} соответствует члену [S] {А} в (5.7Ь), поэтому можно определить {F} как соответствующее выражению [Е]е в (5.7Ь). Однако [Е]е можно рассматривать как начальные напряжения а , которые в данном случае представляют собой напряжения, обусловленные энергетически эквивалентной нагрузкой. При этом следует учесть, что все же остаются трудности при построении указанного преобразования для многомерных напряженных состояний.

Ранее было показано, что при определенных условиях (например, для стержневого элемента при приложении распределенной нагрузки) можно подсчитать непрерывное точное распределение напряжений, однако практические соображения могут побудить к определению приближенных гистограммных форм распределений напряжений, когда напряжения терпят разрывы при переходе от элемента к элементу. В других случаях (как, например, для треугольных элементов с постоянным значением деформации при приложении к конструкции сосредоточенных сил) численное решение приводит в основном к разрывным распределениям напряжений во всей конструкции. Следовательно, для целей проектирования имеется необходимость в схеме, которая приводила бы к непрерывному представлению поля напряжений. Рациональным образом это можно сделать с помощью введения понятия сопряженных напряжений [9.12]. Реализация этой идеи предполагает использование техники сглаживания, которая обеспечивает непрерывность представлений полей напряжений для согласованных конечно-элементных моделей.

Если для поля перемещений A=[N] {А} функции формы [ N J приводят к согласованному представлению, то простейшей и наиболее естественной согласованной аппроксимацией напряжений может служить соотношение a=[N] {а}, где - согласованное поле напряжений, а {а} включает значения напряжений в заданных точках. Будем называть это представление совместимым с перемещениями. Конечно, можно выбрать согласованное представление напряжений, которое не является совместимым с перемещениями, однако для этого требуются дополнительные рассмотрения, не использующие результаты проведенных вычислений. Стандартный расчет сопряженных напряжений основан на том, что напряжения согласованы и совместимы с перемещениями. Заметим, что а может включать три компоненты в случае плоского напряженного состояния (о, Оу, ху), поэтому [N] - прямоугольная матрица.

Согласно теории для аппроксимации сопряженных напряжений, необходимо образовать два типа матриц для элементов. Пер-