Очевидно, что перечисление компонент вектора в виде столбца невыгодно с типографской точки зрения, поэтому мы будем записывать

эти компоненты в виде вектор-строки, обозначаемой символом .

Транспонированную матрицу определим как матрицу, получаемую заменой ее строк на столбцы. Согласно этому определению, при транспонировании вектор-столбца получается вектор-строка и наоборот. Так, обозначая транспонирование латинским верхним индексом Т, можем записать рассматриваемые векторы в следующем виде:

Отдельная компонента произвольного вектора, задающего п перемещений в узле {А}= L Ai--.Ai.--An J . например Aj, называется i-u степенью свободы.

Первым шагом на пути определения векторов сил и перемещений является задание узловых точек и их расположения относительно координатных осей. В методе конечных элементов следует различать глобальные и локальные системы координат, а также системы координат с началом в узловых точках. Глобальные оси координат задаются для всей конструкции, описываемой многими конечными элементами. Локальные (или элементные) оси координат связаны с отдельными элементами. Так как элементы, вообще говоря, различным образом ориентированы друг относительно друга (ситуация наглядно отражена в гл. 1 при изложении примеров численного анализа авиационных конструкций, судов и реакторов), то локальные оси координат также в общем случае различно ориентированы. На рис. 2.2(a) локальная система координат обозначена штрихами. И наконец, ориентации систем координат, определенных в точках соединения элементов, различны, вообще говоря, для некоторых или для всех элементов, соединенных этой точкой. Эти оси координат отмечаются двумя штрихами. В книге координаты помечаются одни.м и двумя штрихами только в том случае, если различные координатные системы сравниваются или появляются в одном и том же месте текста. Если же рассматривается одна из координатных систем, то штрихи не пишутся.

Локальные координаты используются в большинстве случаев при формулировке уравнений для отдельных элементов, и ниже описываются способы введения локальных координат для элементов и нумерации узлов элемента. Глобальные координаты фигурируют в основном в гл. 3 при выводе в разд. 3.1 и 3.2 уравнений для всей конструкции (глобальные уравнения). Значение и характер применения координат с началом в узловых точках становятся ясными в п. 3.5.3.

На рис. 2.2(b) изображен принятый в книге способ введения систем координат и нумерации узлов для плоских конечных элементов. Ближайший к началу координат или совпадающий с ним узел принимается за узел 1. Далее следующему в положительном направлении оси X узлу на плоскости х - у присваивается номер 2.

Оси координат с началам в узлах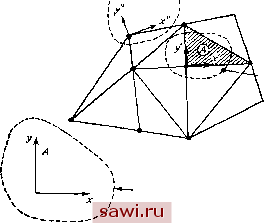

Глодальиые оси

/!окальные оси для элепента А

Рнс. 2.2. Оси координат и правило нумерации узлов, (а) Типы координатных осей, (Ь) оси координат и правило нумерации узлов.

Способ нумерации соответствует движению против часовой стрелки. Так определяются плоские элементы (пластинчатые в плоском напряженном состоянии или при изгибе, а также элементы в случае плоской деформации), лежащие в плоскости х - у. Иначе нумеруются элементы поперечных сечений осесимметричных тел. Правила для нумерации узлов в трехмерных элементах аналогичны вышеприведенным.

Зная основные свойства упругого поведения конечного элемента или конструкции в локальной системе координат, можно легко осуществить преобразование сил и перемещений к глобальной системе координат.

2.2. Идеализация с помощью основных конечных элементов

2.2. Идеализация с помощью основных конечных элементов

Для того чтобы оценить значение различных альтернативных подходов при формулировке конечно-элементных соотношений, полезно изучить взаимосвязь между простой моделью поведения конечного элемента и поведением реальной конструкции. Эта модель наглядно характеризует поведение элемента, хотя существуют и другие равноценные способы рассмотрения основополагающих концепций метода конечных элементов. Действительно, подход, основанный на энергетических или вариационных принципах (гл. 6),- это, по-видимому, наиболее широко используемая схема реализации метода конечных элементов. Однако в этом подходе основополагающие концепции метода конечных элементов рассматриваются с других позиций, нежели в настоящей главе.

Для рассматриваемой здесь простой модели каждому конечному элементу в реальной конструкции отвечает распределенное поле напряжений. Однако для построения математической модели напряженное состояние представляется силами - обобщенными силами - в точках соединения, или узлах элементов. Соответственно смещения этих точек - степени свободы - используются для описания перемещений элемента.

Реальное и идеализированное поведения типичного элемента сравниваются на рис. 2.3. Действительное распределение напряжений на границе элемента изображено на рис. 2.3(a); действительные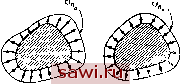

Рис. 2.3 Конечно-элементное представление поведения тела, (а) Реальное поведение (о - реальное нормальное напряжение), (Ь) основной этап идеализации (а .- идеализированное нормальное напряжение); (с) идеализация, необходимая на этапе расчетов

смещения имеют такой же нерегулярный характер. На рис. 2.3(b) показан основной этап идеализации, а именно непосредственное представление предполагаемого поведения элемента. Считается, что поля напряжений, деформаций и перемещений имеют упрощенный вид. И наконец, на рис. 2.3(c) показана идеализация, необходимая на этапе проведения расчетов. Здесь распределенные вдоль края напряжения заменены обобщенными силами в узлах. Таким образом, процесс построения соотношений в методе конечных элементов